【题目】如图,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,DC=3,动点P从点A出发,沿A→D→C→B方向移动,动点Q从点A出发,在AB边上移动.设点P移动的路程为x,点Q移动的路程为y,线段PQ平分梯形ABCD的周长.
(1)求y与x的函数关系式,并求出x,y的取值范围;
(2)当PQ∥AC时,求x,y的值;
(3)当P不在BC边上时,线段PQ能否平分梯形ABCD的面积?若能,求出此时x的值;若不能,说明理由.
参考答案:
【答案】
(1)
解:过C作CE⊥AB于E,则CD=AE=3,CE=4,可得BC=5,
所以梯形ABCD的周长为6+3+4+5=18,
∵PQ平分ABCD的周长,
∴x+y=9,
∵0≤y≤6,
∴3≤x≤9,
故所求关系式为:y=﹣x+9,3≤x≤9;

(2)
解:依题意,P只能在BC边上,7≤x≤9.
PB=12﹣x,BQ=6﹣y,
因为PQ∥AC,所以△BPQ∽△BCA,所以 ![]() ,
,
得: ![]() ,
,
即6x﹣5y=42,
解方程组 ![]()
得 ![]() ;
;
(3)
解:梯形ABCD的面积为18,
当P不在BC边上,则3≤x≤7,
a)当3≤x<4时,P在AD边上,S△APQ= ![]() xy,
xy,
如果线段PQ能平分梯形ABCD的面积,则有 ![]() ,
,
可得: ![]() ,
,
解得 ![]() ,
, ![]() (舍去),
(舍去),
b)当4≤x≤7时,点P在DC边上,此时SADPQ= ![]() ×4(x﹣4+y),
×4(x﹣4+y),
如果线段PQ能平分梯形ABCD的面积,则有 ![]() ×4(x﹣4+y)=9,
×4(x﹣4+y)=9,
可得 ![]() 此方程组无解.
此方程组无解.
所以当x=3时,线段PQ能平分梯形ABCD的面积.

【解析】(1)过C作CE⊥AB于E,由勾股定理求得BC的值,进而得到梯形的周长为18,由题意知,y=﹣x+9,由于点Q只在AB上,于是能确定出x的取值范围;(2)∵PQ∥AC,∴△BPQ∽△BCA,有 ![]() ,得6x﹣5y=42,与y=﹣x+9组成方程组求解即可;(3)通过讨论点P的位置,建立关于x,y的方程组求得x的值.
,得6x﹣5y=42,与y=﹣x+9组成方程组求解即可;(3)通过讨论点P的位置,建立关于x,y的方程组求得x的值.
【考点精析】利用解二元一次方程组和函数关系式对题目进行判断即可得到答案,需要熟知二元一次方程组:①代入消元法;②加减消元法;用来表示函数关系的数学式子叫做函数解析式或函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.

(1)发现:如图1,当E点旋转到DA的延长线上时,△ABE与△ADG的面积关系是:;
(2)引申:当正方形AEFG旋转任意一个角度时,△ABE与△ADG的面积关系是:;
(3)如图3,四边形ABMN、四边形DEAC、四边形BFGC均为正方形,则S△ABC、S△AEN、S△BMF、S△DCG的关系是;
(4)运用:某小区中有一块空地,要在其中建三个正方形健身场所(如图3),其余空地修成草坪.若已知其中一个正方形的边长为5m,另一个正方形的边长为4m,则草坪的最大面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.

(1)求证:BP=DP;
(2)如图2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连接,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车为1440辆;当每辆次小车的停车费超过5元时,每增加1元,到此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费一每天的固定支出)
A型利润
B型利润
甲店
200
170
乙店
160
150
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 ()

A.30°
B.50°
C.90°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为6的⊙O沿AB折叠,弧AB与AB垂直的半径OC交于点D且CD=2OD,则折痕AB的长为( )

A.
B.
C.6
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
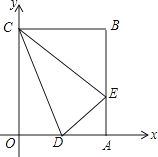
A.(3,1)
B.(3, )
)
C.(3, )
)
D.(3,2)
相关试题

