【题目】如图，二次函数y=ax2的图象与一次函数y=x+b的图象相交于A（﹣2，2）、B两点，从点A和点B分别引平行于y轴的直线与x轴分别交于C，D两点，点P（t，0），为线段CD上的动点，过点P且平行于y轴的直线与抛物线和直线分别交于R，S．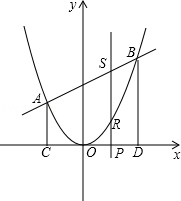

（1）求一次函数和二次函数的解析式，并求出点B的坐标；
（2）当SR=2RP时，计算线段SR的长；
（3）若线段BD上有一动点Q且其纵坐标为t+3，问是否存在t的值，使S△BRQ=15？若存在，求t的值；若不存在，说明理由．

参考答案：

【答案】
（1）

解：由题意知点A（﹣2，2）在y=ax2的图象上，又在y=x+b的图象上

所以得2=a（﹣2）2和2=﹣2+b，

∴ ，b=4．

∴一次函数的解析式为y=x+4．

二次函数的解析式为y= x2．

由 ，

解得 或 ，

所以B点的坐标为（4，8）


（2）

解：因过点P（t，0）且平行于y轴的直线为x=t，

得 ，

所以点S的坐标（t，t+4）．

由 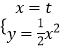得 ，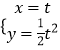

所以点R的坐标（t， t2）．

所以SR=t+4﹣ t2，RP= t2．

由SR=2RP得t+4﹣ t2=2× t2，

解得 或t=2．

因点P（t，0）为线段CD上的动点，

所以﹣2≤t≤4，

所以 或t=2

当t=2时，SR=2+4﹣ ×22=4

所以线段SR的长为 或4


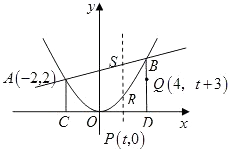
（3）

解：存在符合题意的t．

因BQ=8﹣（t+3）=5﹣t，点R到直线BD的距离为4﹣t，

所以S△BRQ= （5﹣t）（4﹣t）=15．

解得t=﹣1或t=10．

因为﹣2≤t≤4，

所以t=﹣1．


【解析】（1）将A点坐标分别代入抛物线和直线的解析式中即可求出两函数的解析式．然后联立两函数的函数式即可求出B点的坐标．（2）线段SR实际是直线AB的函数值和抛物线函数值的差．而RP的长实际是R点的纵坐标，根据SR=2RP可得出一个关于P点横坐标t的方程，据此可求出P点的横坐标t．然后代入SR的表达式即可求出SR的长．（3）可用t表示出BQ的长，再根据D，P的坐标用t表示出R到BD的距离，然后根据三角形的面积公式即可得出△BRQ的面积表达式，根据其面积为15可求出t的值．

关闭