【题目】已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)求证:G为CD的中点.
(2) 若CF=2,AE=3,求BE的长;
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)通过证△ECG≌△DCF得到CG=CF,结合已知条件知CG=![]() CD,即G为CD的中点.
CD,即G为CD的中点.
(2)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可.
试题解析:(1)证明:如图,∵点F为CE的中点,
∴CF=![]() CE
CE
在△ECG与△DCF中,
∠2=∠1、∠C=∠C、CE=CD,
∴△ECG≌△DCF(AAS),
∴CG=CF=![]() CE.
CE.
又CE=CD,
∴CG=![]() CD,即G为CD的中点;
CD,即G为CD的中点;
(2)∵CE=CD,点F为CE的中点,CF=2,
∴DC=CE=2CF=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥BC,
∴∠AEB=90,
在Rt△ABE中,由勾股定理得:BE=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB=
 °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解. (1)若
 =30,则∠AOC=________.
=30,则∠AOC=________. (2)若
 =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数; (3)若0<
 <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用  的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(﹣2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.
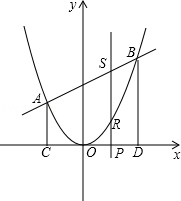
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S△BRQ=15?若存在,求t的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值
(单位:g) 5
5 2
20
1
3
6
袋 数
1
4
3
4
5
3
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
-
科目: 来源: 题型:
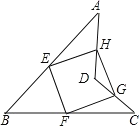
查看答案和解析>>【题目】如图,E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状,并说明你的理由;
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形?证明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在进行二次根式化简时,我们有时会碰上如
 ,
, ,
,  一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: =
= (一),
(一), (二),
(二), (三),
(三), 还可以用以下方法化简:
还可以用以下方法化简:  =
= (四)
(四)以上这种化简的方法叫做分母有理化。
(1)请化简
 =___.
=___.(2)若a是
 的小数部分则
的小数部分则 =___.
=___.(3)矩形的面积为
 ,一边长为
,一边长为 ,则它的周长为___.
,则它的周长为___.(4)化简
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

相关试题

