【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
x(元/件) | 35 | 40 | 45 | 50 | 55 |
y(件) | 550 | 500 | 450 | 400 | 350 |
(1)试求y与x之间的函数表达式;
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价﹣成本总价);
(3)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?最大毛利润是多少?此时每天的销售量是多少?
参考答案:
【答案】
(1)解:解法1:设y与x之间的函数关系满足y=kx+b
把x=40,y=500;x=50,y=400
分别代入上式得:
![]() ,
,
解得 ![]()
∴y=﹣10x+900
∵表中其它对应值都满足y=﹣10x+900
∴y与x之间的函数关系为一次函数,且函数表达式为y=﹣10x+900(30≤x≤80);
解法2:设y与x之间的函数关系满足y=ax2+bx+c
把x=35,y=550;x=40,y=500;x=50,y=400分别代入上式
得 
解,得  ∴y=﹣10x+900
∴y=﹣10x+900
∵表中其它对应值都满足y=﹣10x+900
∴y与x之间的函数关系为一次函数,且函数表达式为y=﹣10x+900(30≤x≤80)
(2)解:方法1:毛利润S=(x﹣30)y
=(x﹣30)(﹣10x+900)
=﹣10x2+1200x﹣27000(30≤x≤80)
方法2:毛利润S=xy﹣30y
=x(﹣10x+900)﹣30×(﹣10x+900)
=﹣10x2+1200x﹣27000(30≤x≤80)
(3)解:在S=﹣10x2+1200x﹣27000中
∵a=﹣10<0,∴当 ![]() 时
时
∴S最大=﹣10×602+1200×60﹣27000=9000(元)
此时每天的销售量为:y=﹣10×60+900=300(件).
∴当销售单价定为60元/件时,该公司试销这种产品每天获得的毛利润最大,最大毛利润是9000元,此时每天的销售量是300件
【解析】(1)方法一,根据图中表格可知:每天的销售单价x增加5元,销售量y减少50件,故每天的销售量y和销售单价x之间为一次函数的关系,故可用待定系数法将y与x之间的函数表达式求出;方法二,设y与x之间满足二次函数表达式,将表格中任意三个值代入,可将该函数求出;(2)方法一,根据:毛利润=(每件产品的销售价﹣成本)×销售量,可求出S与x之间的函数表达式;方法二,根据:毛利润=销售总价﹣成本总价,也可求出S与x之间的函数表达式;(3)由(2)知,当x=﹣ ![]() 时,二次函数能取得极值.
时,二次函数能取得极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
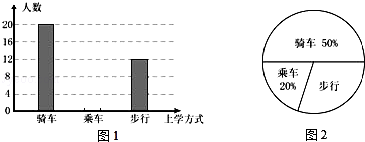
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
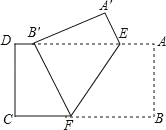
(1)求证:B′E=BF;
(2)求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
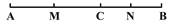
(1)若AC =9cm,CB = 6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB =
 cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗? (3)若C在线段AB的延长线上,且满足AC
 BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOB=
 °,过点O作OB⊥OC.请画图示意并求解.
°,过点O作OB⊥OC.请画图示意并求解. (1)若
 =30,则∠AOC=________.
=30,则∠AOC=________. (2)若
 =40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数;
=40,射线OE平分∠AOC , 射线OF平分∠BOC , 求∠EOF的度数; (3)若0<
 <180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用
<180,射线OE平分∠AOC , 射线OF平分∠BOC , 则∠EOF=________°.(用  的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(﹣2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.
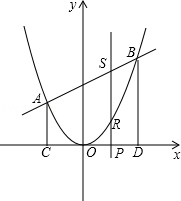
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S△BRQ=15?若存在,求t的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值
(单位:g) 5
5 2
20
1
3
6
袋 数
1
4
3
4
5
3
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
相关试题

