【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

参考答案:
【答案】(1)130°;(2)①90![]() -
-![]() ;②不变,90
;②不变,90![]() -
-![]() ;③∠NDC+∠MDB=90
;③∠NDC+∠MDB=90![]() -
-![]() .
.
【解析】
(1)根据已知,以及三角形内角和等于180![]() ,即可求解;
,即可求解;
(2)①根据平行线的性质可以证得∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,再利用含有
,再利用含有![]() 的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
②延长BD交AC于点E,则∠NDE=∠MDB,因此∠NDC-∠MDB=∠NDC-∠NDE=∠EDC,再利用三角形内角和为180![]() ,即可求解;
,即可求解;
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,利用平角的定义,即可求解代数式.
-∠BDC,利用平角的定义,即可求解代数式.
解:(1)∵∠A=80![]()
∴∠ABC+∠ACB=180![]() -80
-80![]() =100
=100![]()
又∵ BD平分∠ABC,CD平分∠ACB,
∴∠DBC+∠DCB=![]() 100
100![]() =50
=50![]() .
.
∴ ∠BDC=180![]() -50
-50![]() =130
=130![]() .
.
(2)①∵MN//AB,BD平分∠ABC,CD平分∠ACB,
∴∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,
,
∴ ∠NDC=180![]() -
-![]() -
-![]() ∠ACB,∠MDB=
∠ACB,∠MDB=![]() ∠ABC,
∠ABC,
∴∠NDC-∠MDB=180![]() -
-![]() -
-![]() ∠ACB-
∠ACB-![]() ∠ABC=180
∠ABC=180![]() -
-![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() -
-![]() .
.
②不变;延长BD交AC于点E,如图:

∴∠NDE=∠MDB,
∵∠BDC=180![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() +
+![]() ,
,
∴∠NDC-∠MDB=∠NDC-∠NDE=∠EDC=180![]() -∠BDC=180
-∠BDC=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() ,
,
同①,说明MN在旋转过程中∠NDC-∠MDB的度数只与∠A有关系,而∠A始终不变,
故:MN在旋转过程中∠NDC-∠MDB的度数不会发生改变.
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,
-∠BDC,
由②知∠BDC=90![]() +
+![]() ,
,
∴∠NDC+∠MDB=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() .
.
故∠NDC与∠MDB的关系是∠NDC+∠MDB=90![]() -
-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
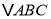 的
的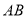 边的异侧作
边的异侧作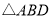 ,并使
,并使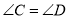 .点
.点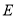 在射线
在射线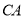 上.
上.(1)如图,若
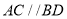 ,求证:
,求证: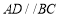 ;
;(2)若
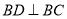 ,试解决下面两个问题:
,试解决下面两个问题:①如图2,
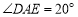 ,求
,求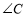 的度数;
的度数;②如图3,若
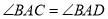 ,过点
,过点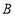 作
作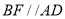 交射线
交射线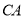 于点
于点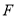 ,当
,当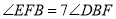 时,求
时,求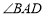 的度数.
的度数.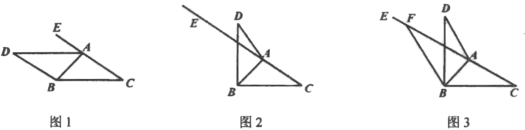
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A. AF=AEB. △ABE≌△AGFC. AF=EFD. BE=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2=
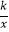 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.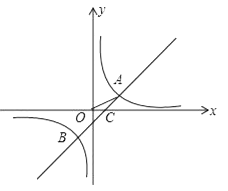
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是时,有y1>y2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形,是因式分解的是()
A.x2-9+6x=(x+3)(x-3)+6xB.(x+5)(x-2)=x2+3x-10
C.x2-8x+16=(x-4)2D.x2+1=x(x+
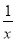 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .
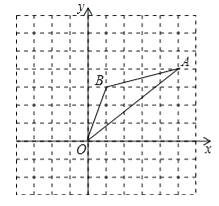
(1)画出△A1OB1;
(2)在旋转过程中点B所经过的路径长为;
(3)求在旋转过程中线段AB、BO扫过的图形的面积之和.
相关试题

