【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2= ![]() 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.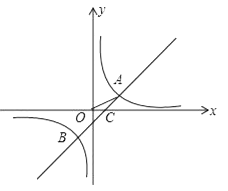
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是时,有y1>y2 .
参考答案:
【答案】
(1)解:将A(2,1)代入y2= ![]() ,1=
,1= ![]() ,
,
解得:k=2,
∴反比例函数解析式为y2= ![]() .
.
将B(n,﹣2)代入y2= ![]() ,﹣2=
,﹣2= ![]() ,
,
解得:n=﹣1,
∴点B的坐标为(﹣1,﹣2)
(2)﹣1<x<0或x>2
【解析】(2)观察函数图象发现:当﹣1<x<0或x>2时,一次函数图象在反比例函数图象上方,∴当x的取值范围是﹣1<x<0或x>2时,有y1>y2.
所以答案是:﹣1<x<0或x>2.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查
B. 该校只有360名家长持反对态度
C. 样本是360名家长
D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
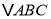 的
的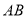 边的异侧作
边的异侧作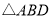 ,并使
,并使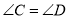 .点
.点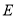 在射线
在射线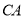 上.
上.(1)如图,若
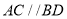 ,求证:
,求证: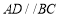 ;
;(2)若
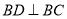 ,试解决下面两个问题:
,试解决下面两个问题:①如图2,
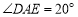 ,求
,求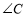 的度数;
的度数;②如图3,若
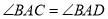 ,过点
,过点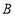 作
作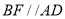 交射线
交射线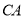 于点
于点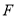 ,当
,当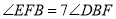 时,求
时,求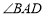 的度数.
的度数.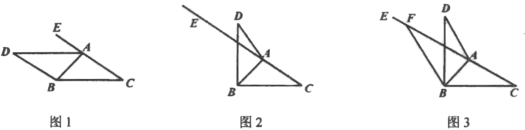
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A. AF=AEB. △ABE≌△AGFC. AF=EFD. BE=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, 平分
平分 ,
, 平分
平分 .
.(1)若
 ,则
,则 的度数为______;
的度数为______;(2)若
 ,直线
,直线 经过点
经过点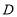 .
.①如图2,若
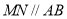 ,求
,求 的度数(用含
的度数(用含 的代数式表示);
的代数式表示);②如图3,若
 绕点
绕点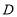 旋转,分别交线段
旋转,分别交线段 于点
于点 ,试问在旋转过程中
,试问在旋转过程中 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出 的度数(用含
的度数(用含 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:③如图4,继续旋转直线
 ,与线段
,与线段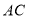 交于点
交于点 ,与
,与 的延长线交于点
的延长线交于点 ,请直接写出
,请直接写出 与
与 的关系(用含
的关系(用含 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形,是因式分解的是()
A.x2-9+6x=(x+3)(x-3)+6xB.(x+5)(x-2)=x2+3x-10
C.x2-8x+16=(x-4)2D.x2+1=x(x+
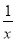 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
相关试题

