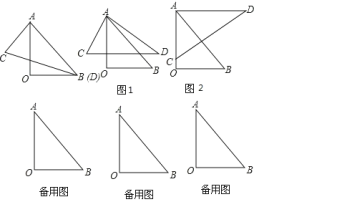
【题目】一副三角板的三个内角分别是90![]() ,45
,45![]() ,45
,45![]() 和90
和90![]() ,60
,60![]() ,30
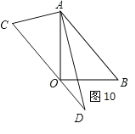
,30![]() ,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0
,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0![]() <α<180
<α<180![]() )
)
(1)如图1中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图2中,当α=___时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数。(写出三个即可)
参考答案:
【答案】(1)15°(2)45°(3)105°或135°或150°或165°或135°或75°或45°或30°
【解析】
(1)由平行内错角相等得:∠AEC=∠B=45°,再由三角形的一个外角等于和它不相邻的两个内角的和可得α=15°;
(2)图3中,直接由平行内错角得出α=∠B=45°;
(3)分别画出图形,根据各图形求出α的值.
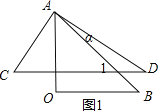
(1)如图1,当∠α=15°,CD∥OB,
∵∠D=30°,∠α=15°,
∴∠1=45°,
∵∠B=45°,
∴∠1=∠B,
∴CD∥OB。
(2)当α=45°时,AD∥OB,
∵∠B=45°,
∴∠α=∠B,
∴AD∥OB;
故答案为:45°.
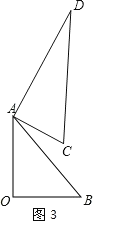
(3)①如图3,AO∥CD
∴∠D+∠DAO=180°,
∴∠BAD=180°45°30°=105°,
∴当α=105°时,CD∥OA;
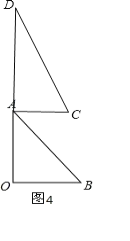
②如图4,AC∥OB
∴∠CAB=∠B=45°,
∴∠BAD=∠CAB+∠CAD=45°+90°=135°,
∴当α=135°时,AC∥OB;
③如图5,DC∥AB
∴∠C=∠BAC=60°,
∴∠BAD=90°+60°=150°,
∴当α=150°时,DC∥AB;
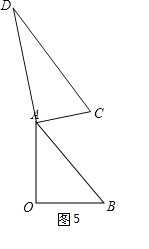
④如图6,DC∥OB
连接BC,
∵DC∥OB,
∴∠DCB+∠OBC=180°,
∵∠ACD=60°,∠OBA=45°,
∴∠ACB+∠ABC=180°60°45°=75°,
∴∠CAB=105°,
∴∠BAD=360°90°105°=165°,
∴当α=165°时,CD∥OB;
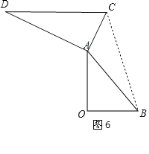
⑤如图7,AD∥OB,
∴∠DAO=∠O=90°,
∴∠BAD=90°+45°=135°,
∴当α=135°时,AD∥OB;
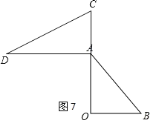
⑥如图8,CD∥OA,
∴∠D=∠DAO=30°,
∴∠BAD=30°+45°=75°,
∴当α=75°时,CD∥OA;

⑦如图9,AC∥OB
∴AO与AD重合,
∴∠BAD=45°,
∴当α=45°时,AC∥OB;
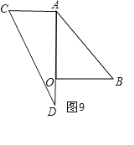
⑧如图10,OC∥AB
∴∠BAD=∠D=30°,
∴当α=30°时,OC∥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载)
B型车(满载)
运货总量
3辆
2辆
38吨
1辆
3辆
36吨
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知 ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形 的周长为___________.
的周长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.

(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数y=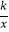 (k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 , 写出符合题意的其中一条抛物线解析式 , 并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把含
 ,
, 角的两块直角三角板放置在同一平面内.若
角的两块直角三角板放置在同一平面内.若 ,
, ,则以
,则以 为顶点的四边形的面积是___________.
为顶点的四边形的面积是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店取厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要800元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件100元,乙种商品的售价为每件125元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于900元,则甲种商品最多可购进多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,∠FMP+∠FPM =∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由


相关试题

