【题目】AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)
(1)当点P在射线FC上移动时,∠FMP+∠FPM =∠AEF成立吗?请说明理由。
(2)当点P在射线FD上移动时,∠FMP+∠FPM与∠AEF有什么关系?并说明你的理由


参考答案:
【答案】(1)成立。…………………………………………………………2分
理由:因为AB∥CD
所以∠AEF十∠EFC=180° (两直线平行同旁内角互补)
因为∠FMP+∠FPM+∠EFC=180° (三角形内角和定理)
所以∠FMP+∠FPM=∠AEF(等量代换)……………………………………………6分
(2)∠FMP+∠FPM与∠AEF互补(∠FMP+∠FPM+∠AEF=180°)……………8分
理由:因为AB∥CD
所以∠AEF=∠EFD(两直线平行,内错角相等)
因为∠FMP+么FPM+∠EFD=180°(三角形内角和定理)
所以∠FMP+∠FPM+∠AEF=180°(等量代换)………………………………l2
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m-3)x|m|-2+3是一次函数,求解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.

(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
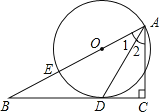
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解为x=2的一元一次方程 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果α、β互为余角,则( )
A. α + β=180° B. α-β=180° C. α-β=90° D. α + β=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利25%元,则这件商品的进价为_______元.
相关试题

