【题目】已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数y= ![]() (k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),他的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 , 写出符合题意的其中一条抛物线解析式 , 并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数 .
参考答案:
【答案】
(1)解:如图1,
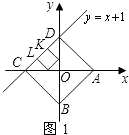
当点A在x轴正半轴,点B在y轴负半轴上时,
∵OC=0D=1,
∴正方形ABCD的边长CD= ![]() ;∠OCD=∠ODC=45°,
;∠OCD=∠ODC=45°,
当点A在x轴负半轴、点B在y轴正半轴上时,
设小正方形的边长为a,
易得CL=小正方形的边长=DK=LK,故3a=CD= ![]() .
.
解得a= ![]() ,所以小正方形边长为
,所以小正方形边长为 ![]() ,
,
∴一次函数y=x+1图象的伴侣正方形的边长为 ![]() 或
或 ![]()
(2)解:如图2,作DE,CF分别垂直于x、y轴,

易知△ADE≌△BAO≌△CBF
此时,m<2,DE=OA=BF=m,OB=CF=AE=2﹣m,
∴OF=BF+OB=2,
∴C点坐标为(2﹣m,2),
∴2m=2(2﹣m),解得m=1.
反比例函数的解析式为y= ![]() .
.
(3)(3,4),y=﹣ ![]() x2+
x2+ ![]() ,偶数
,偶数
【解析】解:(3)实际情况是抛物线开口向上的两种情况中,另一个点都在(3,4)的左侧,而开口向下时,另一点都在(3,4)的右侧,与上述解析明显不符合
①当点A在x轴正半轴上,点B在y轴正半轴上,点C坐标为(3,4)时:另外一个顶点为(4,1),对应的函数解析式是y=﹣ ![]() x2+
x2+ ![]() ;
;
②当点A在x 轴正半轴上,点 B在 y轴正半轴上,点D 坐标为(3,4)时:不存在,
③当点A 在 x 轴正半轴上,点 B在 y轴负半轴上,点C 坐标为(3,4)时:不存在
④当点A在x 轴正半轴上,点B在y轴负半轴上,点D坐标为(3,4)时:另外一个顶点C为(﹣1,3),对应的函数的解析式是y= ![]() x2+
x2+ ![]() ;
;
⑤当点A在x轴负半轴上,点B在y轴负半轴上,点D坐标为(3,4)时,另一个顶点C的坐标是(7,﹣3)时,对应的函数解析式是y=﹣ ![]() ;
;
⑥当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(﹣4,7)时,对应的抛物线为y= ![]() x2+
x2+ ![]() ;
;
∵由抛物线的伴侣正方形的定义知,一条抛物线有两个伴侣正方形,是成对出现的,
∴所求出的任何抛物线的伴侣正方形个数为偶数.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
A,B两种型号车的进货和销售价格表:A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
(1)求今年6月份A型车每辆销售价多少元;
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司现有114吨货物,计划同时租出A,B两种型号的车,王经理发现一个运货货单上的一个信息是:
A型车(满载)
B型车(满载)
运货总量
3辆
2辆
38吨
1辆
3辆
36吨
根据以上信息,解析下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)若物流公司打算一次运完,且恰好每辆车都装满货物,请你帮该物流公司设计租车方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形
 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知 ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形 的周长为___________.
的周长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板的三个内角分别是90
 ,45
,45 ,45
,45 和90
和90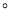 ,60
,60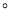 ,30
,30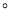 ,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0
,按如图所示叠放在一起,若固定三角形AOB,改变三角形ACD的位置(其中点A位置始终不变),可以摆成不同的位置,使两块三角板至少有一组边平行。设∠BAD=α(0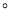 <α<180
<α<180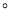 )
)(1)如图1中,请你探索当α为多少时,CD∥OB,并说明理由;
(2)如图2中,当α=___时,AD∥OB;
(3)在点A位置始终不变的情况下,你还能摆成几种不同的位置,使两块三角板中至少有一组边平行,请直接写出符合要求的α的度数。(写出三个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把含
 ,
, 角的两块直角三角板放置在同一平面内.若
角的两块直角三角板放置在同一平面内.若 ,
, ,则以
,则以 为顶点的四边形的面积是___________.
为顶点的四边形的面积是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店取厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要800元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件100元,乙种商品的售价为每件125元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于900元,则甲种商品最多可购进多少件?
相关试题

