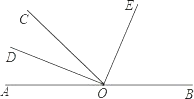
【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
参考答案:
【答案】(1) 154°50′;(2)见解析
【解析】
(1)首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC,再根据∠BOD=∠DOC+∠BOC即可求得答案;
(2)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.
(1)∵∠AOC=50°20′,OD平分∠AOC,
∴∠DOC=![]() ∠AOC=25°10′,∠BOC=180°﹣∠AOC=129°40′,
∠AOC=25°10′,∠BOC=180°﹣∠AOC=129°40′,
∴∠BOD=∠DOC+∠BOC=154°50′;
(2)∵∠DOE=90°,∠DOC=25°10′,
∴∠COE=∠DOE﹣∠DOC=90°﹣25°10′=64°50′.
又∵∠BOE=∠BOD﹣∠DOE=154°50′﹣90°=64°50′,
∴∠COE=∠BOE,
即OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.
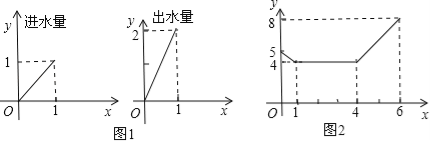
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张长方形的桌子可坐6人,按下图将桌子拼起来.

按这样规律做下去:(1)有5张桌子时可坐 人;
(2)有10张桌子时可坐 人;
(3)有n张桌子可以坐 人(用含有n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
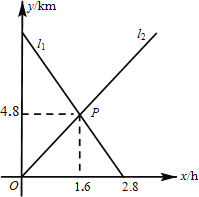
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+7,c=
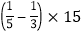 .
.(1)求3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]的值.
(2)若A=
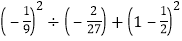 ×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB=
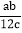 cm,求BC的长.
cm,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )

A.
B.
C.
D.
相关试题

