【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+7,c=![]() .
.
(1)求3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]的值.
(2)若A=![]() ×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB=![]() cm,求BC的长.
cm,求BC的长.
![]()
参考答案:
【答案】(1)﹣126;(2)A>B,理由见解析;(3)BC=2cm
【解析】
(1)先求出a、b、c的值,再把式子化简后代入a、b、c的值即可求解;
(2)先求出A的值,再代入a、b、c的值求出B的值即可比较大小;
(3)先求出AB的长度,再根据比例线段列方程解答即可.
解:a=﹣(﹣2)2×3=﹣4×3=﹣12, b=|﹣9|+7=9+7=16,
c=(![]() )×15=﹣
)×15=﹣![]() ,
,
(1)3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]=3a﹣3(b+c)﹣2b+2(a﹣2c)
=3a﹣3b﹣3c﹣2b+2a﹣4c=5a﹣5b﹣7c,
当a=﹣12,b=16,c=﹣2时,
原式=5×(﹣12)﹣5×16﹣7×(﹣2)=﹣60﹣80+14=﹣126;
(2)A=(﹣![]() )2÷(﹣
)2÷(﹣![]() )+(1﹣
)+(1﹣![]() )2×(1﹣3)2
)2×(1﹣3)2
![]()
=![]()
=![]() ;
;
B=|a|﹣b+c=12﹣16+(﹣2)=﹣6,
∴A>B;
(3)AB=![]() .
.
∵CB:BD=2:3,
∴设CB=2x,DB=3x,则DC=CB+DB=5x.
∵点D是线段AC的中点,
∴AD=DC=5x,即AB=8x.
∴8x=8,
∴x=1,
∴BC=2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
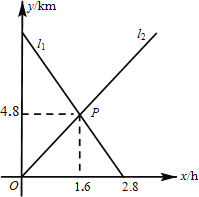
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
-
科目: 来源: 题型:
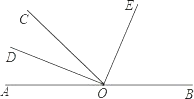
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
已知:如图,直线BC、AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∠4=∠______(______)
又∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE(等式的性质)
即∴∠3=∠______(等量代换)
∴AD∥BE(______).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若平行四边形的一边长为7,则它的两条对角线长可以是( )
A. 12和2 B. 3和4 C. 14和16 D. 4和8
相关试题

