【题目】一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.
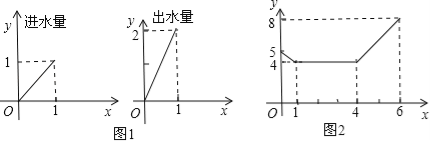
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
参考答案:
【答案】1)0到1分,打开一个进水管,打开一个出水管,1分到4分,两个进水管和一个出水管全部打开,4分到6分,打开两个进水管,关闭出水管;(2)y=2x-4;(3)16升.
【解析】
解:(1) 0到1分,打开一个进水管, 打开一个出水管
1分到4分,两个进水管和一个出水管全部打开
4分到6分,打开两个进水管,关闭出水管……………………3分
(2)当4≤x≤6时,函数图象过点(4,4)(6,8). ………………………1分
设解析式为![]() ,依题意得:
,依题意得:![]() ………………………2分
………………………2分
解得:![]() ………………………4分
………………………4分
∴函数解析式为![]() ………………………5分
………………………5分
(3)若同时打开一个进水管,一个出水管,则10分钟时容器的水量是8+(-1)×4=4升
…………………… 2分
若同时打开两个进水管,则10分钟时容器的水量是8+2×4=16升……………4分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的
 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )

A.(35 +55)m
+55)m
B.(25 +45)m
+45)m
C.(25 +75)m
+75)m
D.(50+20 )m
)m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一张长方形的桌子可坐6人,按下图将桌子拼起来.

按这样规律做下去:(1)有5张桌子时可坐 人;
(2)有10张桌子时可坐 人;
(3)有n张桌子可以坐 人(用含有n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
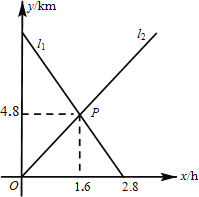
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
-
科目: 来源: 题型:
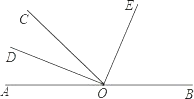
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
相关试题

