【题目】在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:设AE=xm,在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面50m,
∴OE=50m,
∴OP′=OP=PE+OE=x+50,
∵∠P′AE=60°,
∴P′E=tan60°AE= ![]() x,
x,
∴OP′=P′E﹣OE= ![]() x﹣50,
x﹣50,
∴x+50= ![]() x﹣50,
x﹣50,
解得:x=50( ![]() +1)(m),
+1)(m),
∴PO=PE+OE=50( ![]() +1+50=50
+1+50=50 ![]() +100(m),
+100(m),
即飞艇离开湖面的高度是(50 ![]() +100)m;
+100)m;
故选:D.
【考点精析】认真审题,首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角).
-
科目: 来源: 题型:
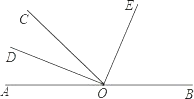
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°20′,OD平分∠AOC,∠DOE=90°.
(1)求∠DOB的度数;
(2)请你通过计算说明OE是否平分∠COB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+7,c=
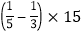 .
.(1)求3[a﹣(b+c)]﹣2[b﹣(a﹣2c)]的值.
(2)若A=
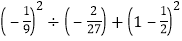 ×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.
×(1﹣3)2,B=|a|﹣b+c,试比较A和B的大小.(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB=
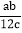 cm,求BC的长.
cm,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
已知:如图,直线BC、AF相交于点E,AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∠4=∠______(______)
又∵∠3=∠4(已知)
∴∠3=∠______(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE(等式的性质)
即∴∠3=∠______(等量代换)
∴AD∥BE(______).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若平行四边形的一边长为7,则它的两条对角线长可以是( )
A. 12和2 B. 3和4 C. 14和16 D. 4和8
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
相关试题

