【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是多少;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
参考答案:
【答案】解:(1)4个小球中有2个红球,
则任意摸出1个球,恰好摸到红球的概率是![]() ;
;
故答案为:![]() ;
;
(2)列表如下:
红 | 红 | 白 | 黑 | |
红 | ﹣﹣﹣ | (红,红) | (白,红) | (黑,红) |
红 | (红,红) | ﹣﹣﹣ | (白,红) | (黑,红) |
白 | (红,白) | (红,白) | ﹣﹣﹣ | (黑,白) |
黑 | (红,黑) | (红,黑) | (白,黑) | ﹣﹣﹣ |
所有等可能的情况有12种,其中两次都摸到红球有2种可能,
则P(两次摸到红球)=![]() =
=![]() .
.
【解析】(1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率;
(2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.



(1)完成下表:
n
1
2
3
4
…
S
1
3
_____
_____
…
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
-
科目: 来源: 题型:
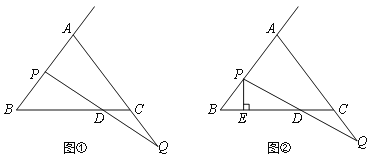
查看答案和解析>>【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
相关试题

