【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
参考答案:
【答案】证明:(1)∵BE∥AD,
∴∠E=∠ADE,
∵∠BAD=∠E,
∴∠BAD=∠ADE,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠CAD=∠ADE,
∴ED∥AC;
(2)连接AE,
∵∠CAD=∠ADE,∠ADE=∠ABE,
∴∠CAD=∠ABE,
∵∠ADC+∠ADB=180°,∠ADB+∠AEB=180°,
∴∠ADC=∠AEB,
∴△ADC∽△BEA,
∴AC:AB=CD:AE,
∴ABCD=AEAC.
【解析】(1)由圆周角定理,可得∠BAD=∠E,又由BE∥AD,易证得∠BAD=∠ADE,然后由AD是△ABC的角平分线,证得∠CAD=∠ADE,继而证得结论;
(2)首先连接AE,易得∠CAD=∠ABE,∠ADC=∠AEB,则可证得△ADC∽△BEA,然后由相似三角形的对应边成比例,证得结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是多少;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】棱长为a的小正方体,按照如图所示的方法一直维续摆放,自上而下分别叫第1层、第2层、……第n(n>0)层,第n层的小方体的个数记为S.



(1)完成下表:
n
1
2
3
4
…
S
1
3
_____
_____
…
(2)上述活动中,自变量和因变量分别是什么?
(3)研究上表可以发现S随n的增大而增大,且有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
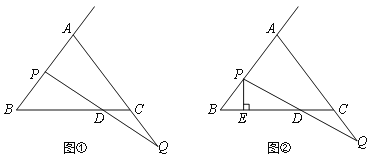
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明袋子中装有颜色不同的黑、白两种球共40个球,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.如图是“摸到白球”的频率折线统计图:
(1)根据统计图,估算盒子里黑、白两种颜色的球各多少个?
(2)如果要使摸到白球的概率为
 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?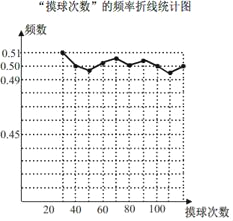
-
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
 ≈1.7)
≈1.7)
相关试题

