【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
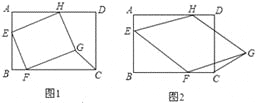
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
参考答案:
【答案】(1)10;(2)12-a;(3)不能
【解析】解:(1)过点G作GM⊥BC于M.在正方形EFGH中,
∠HEF=90°,EH=EF,
∴∠AEH+∠BEF=90°.
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF.
又∵∠A=∠B=90°,
∴△AHE≌△BEF.
同理可证△MFG≌△BEF.
∴GM=BF=AE=2.∴FC=BC-BF=10.
∴![]() .
.
(2)过点G作GM⊥BC交BC的延长线于M,连接HF.
∵AD∥BC,∴∠AHF=∠MFH.
∵EH∥FG,∴∠EHF=∠GFH.
∴∠AHE=∠MFG.
又∵∠A=∠GMF=90°,EH=GF,
∴△AHE≌△MFG.∴GM=AE=2.
∴![]() .
.
(3)△GFC的面积不能等于2.
说明一:∵若S△GFC=2,则12-a=2,∴a=10.
此时,在△BEF中,
![]() .
.
在△AHE中,
![]() ,
,
∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.
说明二:△GFC的面积不能等于2.∵点H在AD上,
∴菱形边EH的最大值为![]() ,∴BF的最大值为
,∴BF的最大值为![]() .
.
又∵函数S△GFC=12-a的值随着a的增大而减小,
∴S△GFC的最小值为![]() .
.
又∵![]() ,∴△GFC的面积不能等于2.
,∴△GFC的面积不能等于2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区
 . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形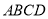 的边
的边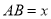 米,面积为
米,面积为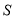 平方米.
平方米.(1)请写出活动区面积
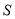 与
与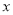 之间的关系式,并指出
之间的关系式,并指出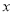 的取值范围;
的取值范围;(2)当
 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
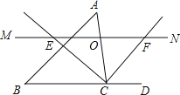
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写证明的理由:
已知,如图AB∥CD,EF、CG分别是∠ABC、∠ECD的角平分线.
求证:EF∥CG
证明:∵AB∥CD(已知)
∴∠AEC=∠ECD( )
又EF平分∠AEC、CG平分∠ECD(已知)
∴∠1=
 ∠ ,∠2=
∠ ,∠2= ∠ (角平分线的定义)
∠ (角平分线的定义)∴∠1=∠2( )
∴EF∥CG( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形
 中,点
中,点 为
为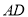 边中点,点
边中点,点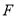 为
为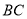 边中点;点
边中点;点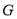 ,
, 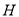 为
为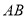 边三等分点,
边三等分点, 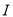 ,
, 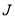 为
为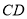 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形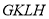 的面积与图3中四边形
的面积与图3中四边形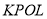 的面积相等吗?
的面积相等吗?(1)小瑞的探究过程如下
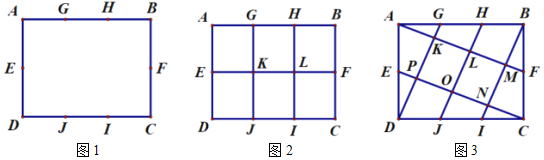
在图2中,小瑞发现,
 ;
;在图3中,小瑞对四边形
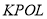 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:设
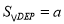 ,
, 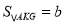
∵
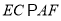
∴
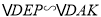 ,且相似比为
,且相似比为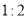 ,得到
,得到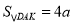
∵
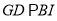
∴
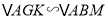 ,且相似比为
,且相似比为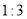 ,得到
,得到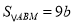
又∵
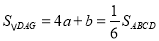 ,
, 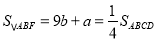
∴
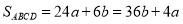
∴
 ,
, 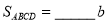 ,
, 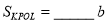
∴
 ,则
,则 (填写“
(填写“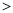 ”,“
”,“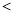 ”或“
”或“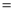 ”)
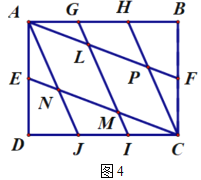
”)(2)小瑞又按照图4的方式连接矩形
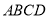 对边上的点.则
对边上的点.则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
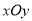 中,二次函数
中,二次函数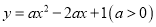 的对称轴为
的对称轴为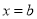 .点
.点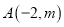 在直线
在直线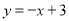 上.
上.(1)求
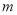 ,
, 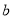 的值;
的值;(2)若点
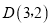 在二次函数
在二次函数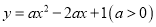 上,求
上,求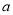 的值;
的值;(3)当二次函数
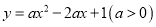 与直线
与直线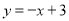 相交于两点时,设左侧的交点为
相交于两点时,设左侧的交点为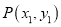 ,若
,若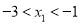 ,求
,求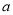 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 的“
的“ 值”定义如下:若点
值”定义如下:若点 为圆上任意一点,线段
为圆上任意一点,线段 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点 的“
的“ 值”,记为
值”,记为 .特别的,当点
.特别的,当点 ,
,  重合时,线段
重合时,线段 的长度为0.
的长度为0.当⊙
 的半径为2时:
的半径为2时:(1)若点
 ,
,  ,则
,则 _________,
_________,  _________;
_________;(2)若在直线
 上存在点
上存在点 ,使得
,使得 ,求出点
,求出点 的横坐标;
的横坐标;(3)直线
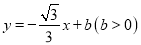 与
与 轴,
轴,  轴分别交于点
轴分别交于点 ,
,  .若线段
.若线段 上存在点
上存在点 ,使得
,使得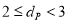 ,请你直接写出
,请你直接写出 的取值范围.
的取值范围.
相关试题

