【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区![]() . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形![]() 的边
的边![]() 米,面积为
米,面积为![]() 平方米.
平方米.
(1)请写出活动区面积![]() 与
与![]() 之间的关系式,并指出
之间的关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?

参考答案:
【答案】(1)S=-2x2+80x(15≤x<40)(2)800
【解析】试题分析:(1)由AB=x,得到BC=80-2x,再由矩形的面积公式即可得出结论;
(2)求出对称轴,进而得到二次函数的最值.
试题解析:解:(1)根据题意得:AB=x,BC=80-2x,∴S=x(80-2x)=80x-2x2.又∵x>0,0<80-2x≤50,解得15≤x<40,∴S=-2x2+80x(15≤x<40);
(2)∵x=![]() =20,∴当x=20时,S=20×(80-20×2)=800.
=20,∴当x=20时,S=20×(80-20×2)=800.
答:当x=20时,活动区的面积最大,活动区的面积最大为800平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,已知
 .
.求作:
 的角平分线
的角平分线 .
.
小霞的作法如下:
(1)如图,在平面内任取一点
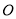 ;
;(2)以点
 为圆心,
为圆心,  为半径作圆,交射线
为半径作圆,交射线 于点
于点 ,交射线
,交射线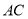 于点
于点 ;
;(3)连接
 ,过点
,过点 作射线
作射线 垂直线段
垂直线段 ,交⊙
,交⊙ 于点
于点 ;
;(4)连接
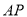 .
.
所以射线
 为所求.
为所求.老师说:“小霞的作法正确.”
请回答:小霞的作图依据是___________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高速公路某收费站出城方向有编号为
 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:收费出口编号





通过小客车数量(辆)
260
330
300
360
240
在
 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,一次函数
中,一次函数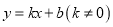 与反比例函数
与反比例函数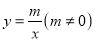 交于点
交于点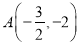 ,
, 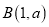 .
.(1)分别求出反比例函数和一次函数的表达式;
(2)根据函数图象,直接写出不等式
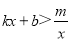 的解集.
的解集.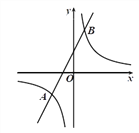
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
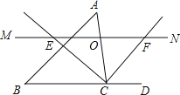
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写证明的理由:
已知,如图AB∥CD,EF、CG分别是∠ABC、∠ECD的角平分线.
求证:EF∥CG
证明:∵AB∥CD(已知)
∴∠AEC=∠ECD( )
又EF平分∠AEC、CG平分∠ECD(已知)
∴∠1=
 ∠ ,∠2=
∠ ,∠2= ∠ (角平分线的定义)
∠ (角平分线的定义)∴∠1=∠2( )
∴EF∥CG( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
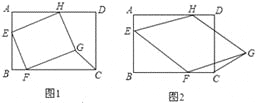
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
相关试题

