搜索
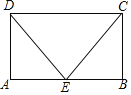
【题目】如图，在矩形ABCD中，E是AB的中点，连接DE、CE．
（1）求证：△ADE≌△BCE；
（2）若AB=6，AD=4，求△CDE的周长．
参考答案：
【答案】（1）证明见解析；（2）16.
【解析】（1）由全等三角形的判定定理SAS即可证得结论；
（2）由（1）中全等三角形的对应边相等和勾股定理求得线段DE的长度，结合三角形的周长公式解答．
（1）在矩形ABCD中，AD=BC，∠A=∠B=90°．
∵E是AB的中点，
∴AE=BE，
在△ADE与△BCE中，
，
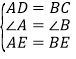∴△ADE≌△BCE（SAS）；
（2）由（1）知：△ADE≌△BCE，则DE=EC，
在直角△ADE中，AE=4，AE=
AB=3，
由勾股定理知，DE=
=5，
∴△CDE的周长=2DE+AD=2DE+AB=2×5+6=16．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，AB=BC=10，以AB为直径作⊙O分别交AC，BC于点D，E，连接DE和DB，过点E作EF⊥AB，垂足为F，交BD于点P．
（1）求证：AD=DE；
（2）若CE=2，求线段CD的长；
（3）在（2）的条件下，求△DPE的面积． -
科目： 来源： 题型：
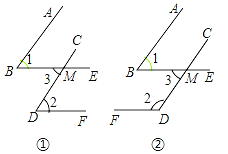
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行，请结合图，探索这两个角之间的关系，并说明理由．
（1）如图①，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（2）如图②，AB∥CD，BE∥DF，∠1与∠2的关系是 ；
证明：
（3）经过上述证明，我们可得出结论，如果一个角的两边与另一个角的两边分别平行，那么这两个角 ；
（4）若这两个角的两边分别平行，且一个角比另一个角的3倍少60°，则这两个角分别是多少度？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠A=
∠B=
∠ACB，CD是△ABC的高，CE是∠ACB的角平分线，求∠DCE的度数。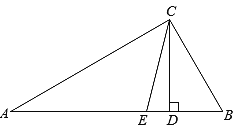
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
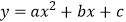与x轴交于两点A（﹣4，0）和B（1，0），与y轴交于点C（0，2），动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒．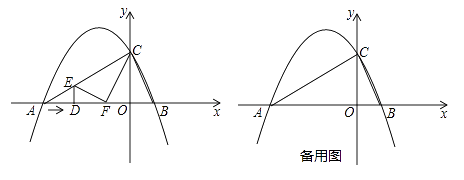
（1）求抛物线的解析式和对称轴；
（2）是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值；若不存在，请说明理由；
（3）设四边形DECO的面积为s，求s关于t的函数表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】“化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化，进而使问题得到解决：
（1）我们知道m2+n2=0可以得到m=0，n=0．如果a2+b2+2a﹣4b+5=0，求a、b的值．
（2）已知a
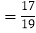x+2017，b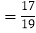x+2015，c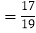x+2016，试问：多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量x的取值有关？若有关请说明理由；若无关请求出多项式的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图棱长为a的小正方体，按照下图的方法继续摆放，自上而下分别叫第一层。第二层……第n层，第n层的小正方体的个数记为S.解答下列问题：
（1）填写表格：
n
1
2
3
4
…
S
1
…
（2）研究上表可以发现S随n的变化而变化，且S随n的增大而增大有一定的规律，请你用式子来表示S与n的关系，并计算当n＝10时，S的值为多少?
相关试题
