【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

参考答案:
【答案】(1)菱形的边长为![]() ;
;
(2)作图见解析.
【解析】试题分析:(1)连接OB、OD和OC,根据菱形、内接圆的性质可得∠DOB=120°,OD=OB=1, CD=BC,∠C=60°,从而得到△COD≌△COB,根据全等三角形的性质,可求得∠COD=∠COB=![]() 、∠DCO=∠BCO=
、∠DCO=∠BCO=![]() ,根据三角形内角和可得△COD 是Rt△COD,由tan∠DCO=
,根据三角形内角和可得△COD 是Rt△COD,由tan∠DCO=![]() 可求得CD的长度,即为所求;(2)根据题意先作出D在BC上的对应点;作出直线a;
可求得CD的长度,即为所求;(2)根据题意先作出D在BC上的对应点;作出直线a;
试题解析:
(1)连接OB、OD和OC,如图所示:

∵半径为1的⊙O经过点A、B、D,且∠A=60°,
∴∠DOB=120°,OD=OB=1,
∵四边形ABCD是菱形,∠A=60°,
∴CD=BC,∠C=60°,
在△COD和△COB中
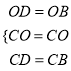
∴△COD≌△COB(SSS),
∴∠COD=∠COB,∠DCO=∠BCO,
∴∠COD=∠COB=![]() ,
,
∠DCO=∠BCO=![]()
∴∠ODC=(180-30-60)o=90o,
∴△COD 是Rt△COD,
∵tan∠DCO=![]()
∴CD=tan30o![]()
∴菱形ABCD的边长是![]() ;
;
(2)如图所示:
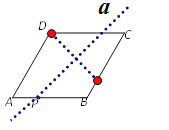
作出D在BC上的对应点,再作出直线a即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(x+2)(x-5)=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①a5a3a=
②(a5)3÷a6= -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由小正方形组成的网格中,点O、M和四边形ABCD的顶点都在格点上.
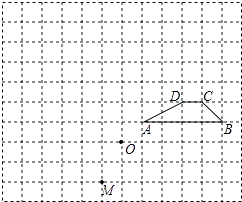
①画出与四边形ABCD关于直线CD对称的图形;
②平移四边形ABCD,使其顶点B与点M重合,画出平移后的图形;
③把四边形ABCD绕点O逆时针旋转180°,画出旋转后的图形. -
科目: 来源: 题型:
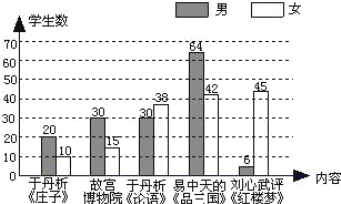
查看答案和解析>>【题目】为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为____名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有____名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的____%;
(4)你认为上述估计合理吗?理由是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.
相关试题

