【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
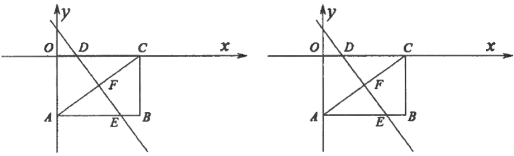
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;拆痕DE的长为
;拆痕DE的长为![]() ; (3)点Q坐标为
; (3)点Q坐标为![]()
【解析】
(1)根据B点的坐标即可求得AC的长度.
(2)首先根据已知条件证明![]() ,再根据相似比例计算DF、CD的长度
,再根据相似比例计算DF、CD的长度
即可计算出D点的坐标,再证明![]() ,根据EF=DF,即可计算的DE的长度.
,根据EF=DF,即可计算的DE的长度.
(3)根据等腰三角形的性质,分类讨论第一种情况当![]() 时;第二种情况当
时;第二种情况当![]() 时;第三种情况当
时;第三种情况当![]() 时,分别计算即可.
时,分别计算即可.
解:(1)![]()
(2)![]() ,由折叠可得:
,由折叠可得:![]()
![]() ,
,![]()
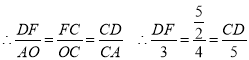 .
.
![]()
![]()
∵四边形OABC是矩形,
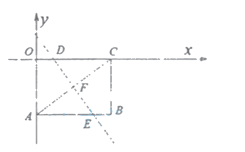
![]()
![]()
![]()
∴拆痕DE的长为![]()
(3)由(2)可知,![]() ,
,
![]()
若以P、D、E、Q为顶点的四边形是菱形,则![]() 必为等腰三角形。
必为等腰三角形。
当![]() 时,可知
时,可知![]() ,
,
此时PE为对角线,可得![]()
当![]() 时,可知
时,可知![]() ,此时DP为对角线,可得
,此时DP为对角线,可得![]() ;
;
当![]() 时,P与C重合,Q与A重合,
时,P与C重合,Q与A重合,![]()
综上所述,满足条件的点Q坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,记
中,记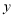 与
与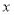 的函数
的函数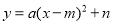 (
(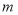 ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与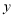 轴交于点
轴交于点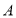 ,当
,当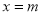 时,函数
时,函数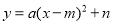 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(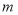 ,
, 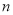 ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
(1)如图,若函数
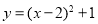 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;(2)如图,若图形G的伴随直线的表达式是
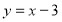 ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求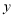 与
与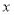 的函数
的函数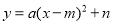 (m>0,n <0)的表达式;
(m>0,n <0)的表达式;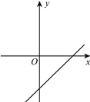
(3)如图,若图形G的伴随直线是
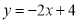 ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.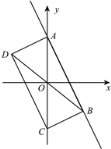
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会干部对校学生会倡导的“牵手特殊教育”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).己知A、B两组捐款人数的比为1: 5.
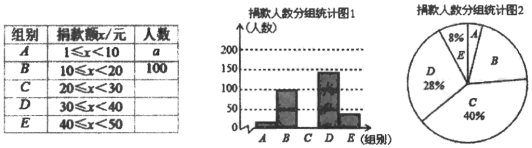
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.
-
科目: 来源: 题型:
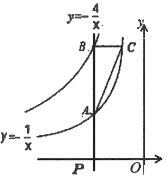
查看答案和解析>>【题目】如图,点
 为
为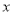 轴负半轴上的一个点,过点
轴负半轴上的一个点,过点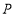 作
作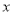 轴的垂线,交函数
轴的垂线,交函数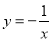 的图像于点
的图像于点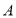 ,交函数
,交函数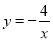 的图像于点
的图像于点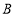 ,过点
,过点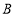 作
作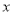 轴的平行线,交
轴的平行线,交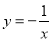 于点
于点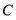 ,连接
,连接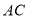 .
.
(1)当点
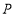 的坐标为(–1,0)时,求
的坐标为(–1,0)时,求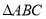 的面积;
的面积;(2)若
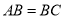 ,求点
,求点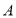 的坐标;
的坐标;(3)连接
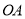 和
和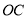 .当点
.当点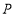 的坐标为(
的坐标为(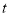 ,0)时,
,0)时,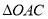 的面积是否随
的面积是否随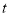 的值的变化而变化?请说明理由.
的值的变化而变化?请说明理由. -
科目: 来源: 题型:
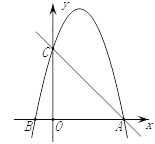
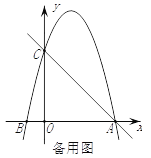
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为_____ cm.
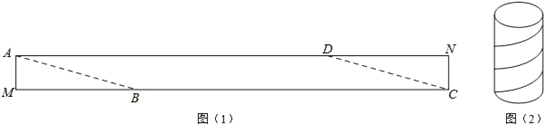
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形
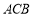 的边
的边 ,等腰直角三角形
,等腰直角三角形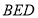 的边
的边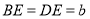 ,且
,且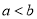 ,点
,点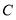 、
、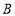 、
、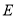 放置在一条直线上,联结
放置在一条直线上,联结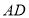 .
.(1)求三角形
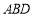 的面积;
的面积;(2)如果点
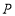 是线段
是线段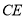 的中点,联结
的中点,联结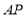 、
、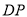 得到三角形
得到三角形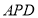 ,求三角形
,求三角形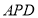 的面积;
的面积;(3)第(2)小题中的三角形
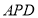 与三角形
与三角形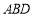 面积哪个较大?大多少?(结果都可用
面积哪个较大?大多少?(结果都可用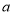 、
、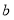 代数式表示,并化简)
代数式表示,并化简)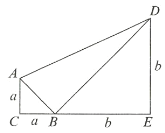
相关试题

