【题目】某中学为了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其它四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了尚不完整的频数分布表:
类别 | 频数(人数) | 频率 |
文学 | m | 0.42 |
艺术 | 22 | 0.11 |
科普 | 66 | n |
其他 | 28 | |
合计 | 1 |
(1)表中m= , n=;
(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最少?
(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?
参考答案:
【答案】
(1)84;0.33
(2)解:由题意可得:最喜爱阅读艺术类读物的学生最少
(3)解:1200名学生中最喜爱阅读科普读物的学生有:1200×0.33=396(人)
【解析】解:(1)由题意可得:22÷0.11=200, 则m=200×0.42=84,
n= ![]() =0.33,
=0.33,
所以答案是:84,0.33;
-
科目: 来源: 题型:
查看答案和解析>>【题目】填在如图各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数
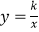 经过正方形AOBC对角线的交点,半径为(4﹣2
经过正方形AOBC对角线的交点,半径为(4﹣2 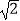 )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 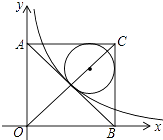
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B分别是反比例函数y=
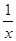 (x>0),y=
(x>0),y= 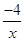 (x<0)的图象上的点,且,∠AOB=90°,则
(x<0)的图象上的点,且,∠AOB=90°,则 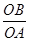 的值为( )
的值为( ) 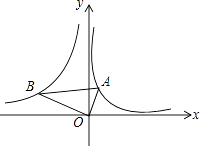
A.4
B.
C.2
D.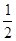
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
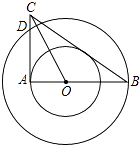
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.
(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)15﹣(﹣8)+(﹣20)﹣12
(2)2×(﹣3)2﹣4×(﹣3)+15
(3)(﹣
 )2+|﹣2|3﹣
)2+|﹣2|3﹣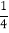
(4)﹣20+(﹣2)2﹣32+|﹣10|
(5)﹣22
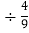 ×
×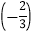 2
2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

相关试题

