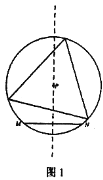
【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
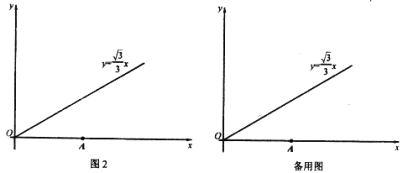
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2![]() ,0),点B在射线y=
,0),点B在射线y=![]() x(x≥0)上。
x(x≥0)上。
(1)在点C(![]() ,0),D(
,0),D(![]() ,1),E(
,1),E(![]() ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.
(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为![]() (0°<
(0°< ![]() ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出![]() 的取值范围是_______________。
的取值范围是_______________。
参考答案:
【答案】(1)D、E;
(2)B(3![]() ,3)。
,3)。
(3)30°< ![]() <90°或
<90°或![]() =150°。
=150°。
【解析】试题分析:(1)用排除法判断;(2) 由题意可知Q点既为线段OA的“三足点”,又是线段OB的“强三足点”,则点Q须满足在OA和OB的垂直平分线上,且∠QOB=30°.
y=![]() x与x轴的夹角为30°.∴∠QOA=60°.设点Q的坐标为(m,n),Q点在OA的垂直平分线上,故m=
x与x轴的夹角为30°.∴∠QOA=60°.设点Q的坐标为(m,n),Q点在OA的垂直平分线上,故m=![]() ,
, ![]() ,QB=QO=
,QB=QO=![]() ,所以B(
,所以B(![]() .
.
(3)这个圆正好过O、Q点,F点坐标为(![]() ,0)由于三足点存在要求等腰三角形顶角≤120度,通过画图可以算出a的范围为:30° <a<90°,及a=150°,此时AK的中垂线与OB的中垂线平行,没有交点根据线段OB的三足点在射线AE和射线QF上,即线段AK的三足点要与这两条射线有交点.
,0)由于三足点存在要求等腰三角形顶角≤120度,通过画图可以算出a的范围为:30° <a<90°,及a=150°,此时AK的中垂线与OB的中垂线平行,没有交点根据线段OB的三足点在射线AE和射线QF上,即线段AK的三足点要与这两条射线有交点.
试题解析:
(1)D、E;
(2)点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,
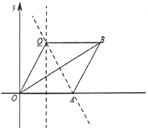
依题可知,∠OQB=120°,∠QOB=30°,∠QOA=60°,
即Q(![]() ,3).
,3).
OQ=BQ=2![]() ,BQ∥OA,
,BQ∥OA,
即B(3![]() ,3).
,3).
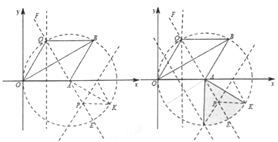
(3)依题可知:
线段OB的三足点在射线AE和射线QF上,
即线段AK的三足点要与这两条射线有交点,
当0< ![]() ≤30°,90°≤
≤30°,90°≤![]() <150°,150°<
<150°,150°< ![]() ≤180°存在交点。
≤180°存在交点。
故若不存在,则30°< ![]() <90°或
<90°或![]() =150°.
=150°.
点睛:在这类问题中,首要的是理解新概念,总结和发现新规律,然后通过模仿,类比或归纳解决问题,关键是理解题中所给的新颖的解题方法,然后利用转化思想根据背景材料将要求的问题转化为阅读得来的方法来解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(2﹣3x)(x+1)
(2)[5xy2(x2﹣3xy)﹣(﹣x2y2)3]÷(5xy)
(3)(x+2)2(x﹣2)2(x2+4)2
(4)(x+y﹣z)(x﹣y+z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:m2﹣m= ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.

(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆中最长的弦为6,则这个圆的半径为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
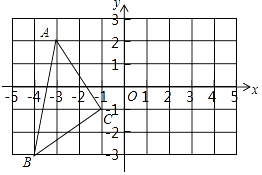
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
相关试题

