【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
参考答案:
【答案】(1)证明见解析;(2)∠F=30°.
【解析】试题分析:连接OD,根据AB=AC得出∠ABC=∠ACB,根据OD=OC得出∠ODC=∠OCD,则∠ABC=∠ODC,从而得出AB∥OD,从而得到切线;连接AD,根据AC为直径得出AD⊥BC,根据DE⊥AB得出△AED和△ADB相似,根据半径得出AB、AC、AE、AD的长度,根据Rt△ADB的三角函数得出∠ABC的度数,从而得出∠F的度数.
试题解析:(1)证明:连接OD.∵AB=AC,∴![]() .∵OD=OC,∴
.∵OD=OC,∴![]() .
.
∴![]() .∴
.∴![]() ∥
∥![]() .∴
.∴![]() .∵DE⊥AB,∴
.∵DE⊥AB,∴![]() .
.
∴![]() .∴
.∴![]() .∴DE是⊙O的切线.
.∴DE是⊙O的切线.
解:连接AD.∵AC为⊙O的直径,∴![]() .
.
又∵DE⊥AB,∴Rt![]() ∽Rt
∽Rt![]() .∴
.∴![]() .∴
.∴![]() .
.
∵⊙O的半径为4,∴AB=AC=8.∴![]() . ∴
. ∴![]() .
.
在Rt![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
又∵AB=AC,∴![]() 是等边三角形.∴
是等边三角形.∴![]() ∴
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC,D为AB中点,DE⊥DF.
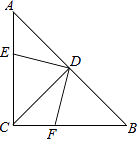
(1)写出图中所有全等三角形,分别为 . (用“≌”符号表示)
(2)求证:ED=DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=
 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y= 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:(1)函数y=
 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x
…
-3
-2
0
1
1.5
2.5
m
4
6
7
…
y
…
2.4
2.5
3
4
6
-2
0
1
1.5
1.6
…
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
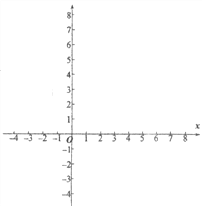
①_____________________________________________;
②____________________________________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(2﹣3x)(x+1)
(2)[5xy2(x2﹣3xy)﹣(﹣x2y2)3]÷(5xy)
(3)(x+2)2(x﹣2)2(x2+4)2
(4)(x+y﹣z)(x﹣y+z) -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:m2﹣m= ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
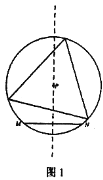
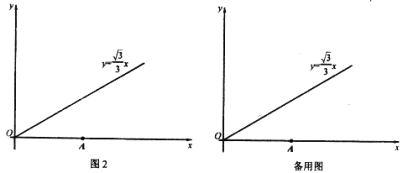
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2
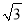 ,0),点B在射线y=
,0),点B在射线y=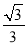 x(x≥0)上。
x(x≥0)上。(1)在点C(
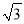 ,0),D(
,0),D(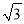 ,1),E(
,1),E(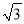 ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为
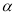 (0°<
(0°< 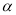 ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出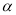 的取值范围是_______________。
的取值范围是_______________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.

(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度.
相关试题

