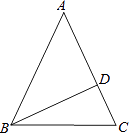
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线. 
(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度.
参考答案:
【答案】
(1)解:)、如图,点P即为所求;

(2)解:∵AD平分∠BAC,
∴∠CAD=∠BAD.
又∵DC⊥AC、DP⊥AB,
∴∠C=∠APD.
在△ACD与APD中,
∵ 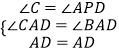 ,
,
∴△ACD≌APD(AAS).
∴AP=AC=4,CD=PD.
在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
设DP为x,则DP=x,BD=3﹣x,在Rt△DPB中,∠DPB=90°,
∴DP2+PB2=DB2,即,x2+12=(3﹣x)2,
解得x= ![]() ,
,
∴CD=DP= ![]() .
.
【解析】(1)过点D作AB的垂线,垂足为P即可;(2)根据角平分线的性质可知∠CAD=∠BAD,利用AAS定理可知△ACD≌APD.在在Rt△ABC中根据勾股定理得出AB的长,设DP为x,则DP=x,BD=3﹣x,在Rt△DPB中,利用勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:m2﹣m= ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
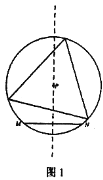
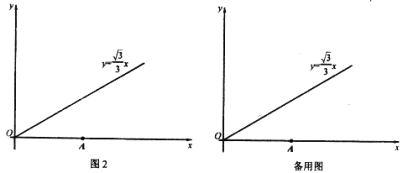
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2
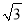 ,0),点B在射线y=
,0),点B在射线y=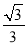 x(x≥0)上。
x(x≥0)上。(1)在点C(
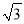 ,0),D(
,0),D(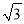 ,1),E(
,1),E(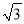 ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为
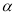 (0°<
(0°< 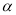 ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出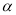 的取值范围是_______________。
的取值范围是_______________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆中最长的弦为6,则这个圆的半径为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
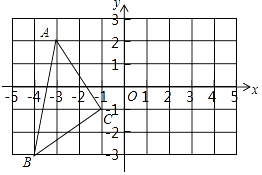
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)
(1)若∠ABD+∠C=120°,求∠A的度数;
(2)若CD=3,BC=5,求△ABC的面积.
相关试题

