【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).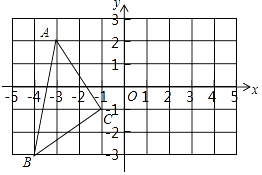
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
参考答案:
【答案】
(1)
解:如图,△A1B1C1即为所求;
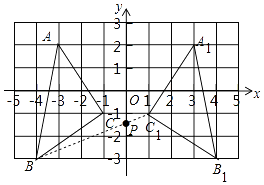
(2)(1,﹣1)
(3)![]()
(4)
解:如图,连接BC1与y轴的交点为P,点P即为所求.

【解析】解:(2.)由图象可知:C1(1,﹣1);
故答案为(1,﹣1).
(3.)S=3×5﹣ ![]() ×1×5﹣
×1×5﹣ ![]() ×2×3﹣
×2×3﹣ ![]() ×2×3=
×2×3= ![]() ;
;
故答案为 ![]() .
.
(1)分别作出点A、B、C关于y轴的对称点A1、B1、C1即可.(2)根据点C1的位置即可解决问题.(3)利用分割法计算即可.(4)连接BC1与y轴的交点即为所求的点P.
-
科目: 来源: 题型:
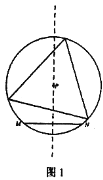
查看答案和解析>>【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
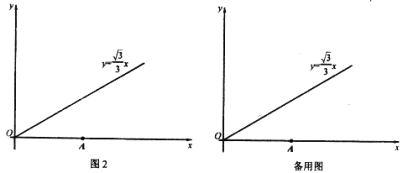
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2
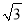 ,0),点B在射线y=
,0),点B在射线y=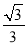 x(x≥0)上。
x(x≥0)上。(1)在点C(
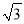 ,0),D(
,0),D(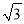 ,1),E(
,1),E(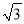 ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为
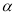 (0°<
(0°< 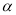 ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出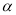 的取值范围是_______________。
的取值范围是_______________。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线.

(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆中最长的弦为6,则这个圆的半径为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BD为高.(从下列问题中任选一问作答)
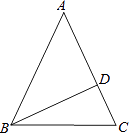
(1)若∠ABD+∠C=120°,求∠A的度数;
(2)若CD=3,BC=5,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
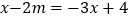 与
与 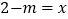 的解互为相反数,求
的解互为相反数,求 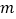 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%,在销售中出现了滞销,于是先后两次降价,售价降为25元.
(1)求这种玩具的进价;
(2)求平均每次降价的百分率(精确到0.1%).
相关试题

