【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC. 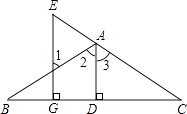
证明:∵AD⊥BC于D,EG⊥BC于G()
∴∠ADC=90°,∠EGC=90°()
∴∠ADC=∠EGC
∴AD∥EG()
∴∠1=∠2()
∠E=∠3()
又∵∠E=∠1()
∴∠2=∠3
∴AD平分∠BAC().
参考答案:
【答案】已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;已知;角平分线的定义
【解析】证明:∵AD⊥BC于D,EG⊥BC于G(已知) ∴∠ADC=90°,∠EGC=90°(垂直的定义)
∴∠ADC=∠EGC
∴AD∥EG(同位角相等,两直线平行)
∴∠1=∠2(两直线平行,内错角相等)
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3
∴AD平分∠BAC(角平分线的定义).
所以答案是:已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;已知;角平分线的定义.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、C、P、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度,若不可能,请说明理由;
②若点Q的速度为每秒0.8cm,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知M=
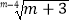 是m+3的算术平方根,N=
是m+3的算术平方根,N=  是n﹣2的立方根, 求:M﹣N的值的平方根.
是n﹣2的立方根, 求:M﹣N的值的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知tanα=0.3249,则α约为( )
A.17°
B.18°
C.19°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2+px-6可以分解为(x+q)·(x-2),那么(p-q)2的值为( )
A. 2 B. 3 C. 4 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C.
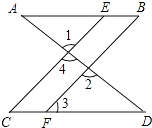
求证:
(1)AB∥CD
(2)∠AEC=∠3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
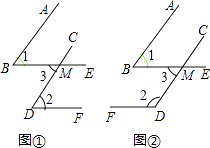
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
相关试题

