【题目】如图,已知∠1=∠2,∠B=∠C. 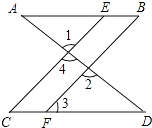
求证:
(1)AB∥CD
(2)∠AEC=∠3.
参考答案:
【答案】
(1)证明:∵∠1=∠2(已知),∠1=∠4(对顶角相等),
∴∠2=∠4(等量替换),
∴CE∥BF(同位角相等,两直线平行),
∴∠3=∠C(两直线平行,同位角相等).
又∵∠B=∠C(已知),
∴∠3=∠B(等量替换),
∴AB∥CD(内错角相等,两直线平行).
(2)证明:∵AB∥CD(已知),
∴∠AEC=∠C(两直线平行,内错角相等).
∵∠B=∠C=∠3(已知),
∴∠AEC=∠3(等量替换).
【解析】(1)由∠1=∠2结合对顶角相等即可得出∠2=∠4,进而可证出CE∥BF,再根据平行线的性质可得出∠3=∠C=∠B,利用平行线的判定定理即可证出AB∥CD;(2)由AB∥CD可得出∠AEC=∠C,结合∠B=∠C=∠3可得出∠AEC=∠3,此题得证.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知tanα=0.3249,则α约为( )
A.17°
B.18°
C.19°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC.
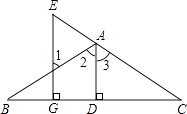
证明:∵AD⊥BC于D,EG⊥BC于G()
∴∠ADC=90°,∠EGC=90°()
∴∠ADC=∠EGC
∴AD∥EG()
∴∠1=∠2()
∠E=∠3()
又∵∠E=∠1()
∴∠2=∠3
∴AD平分∠BAC(). -
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2+px-6可以分解为(x+q)·(x-2),那么(p-q)2的值为( )
A. 2 B. 3 C. 4 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
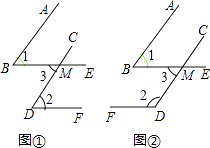
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是什么? 证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程3x2﹣4x+8=0的根的情况是( )
A.有两个相等的实数根B.有两个不相等的实数根
C.只有一个实数根D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式ax2+bx+c=(2x-1)(x+3),求a+b+c的值.
相关试题

