【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、C、P、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度,若不可能,请说明理由;
②若点Q的速度为每秒0.8cm,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
参考答案:
【答案】
(1)
解:∵AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,
∴OA=OC,
又∵矩形ABCD中,AD∥BC.
∴∠OEA=∠FCO,
∴在△AOE和△COF中,

∴△AOE≌△COF(AAS).
∴OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF于点O,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形)
(2)
解:由(1)可知,四边形AFCE是菱形,设AF=FC=CE=AE=x,BF=y,
由题意,有 ![]() 解得
解得 ![]()
即:所求AF的长为5.
(3)
解:①有可能是矩形,理由如下:
当点P从点A出发移动到点B、点Q运动到点D时,四边形APCQ是矩形,
此时,二者的运动时间相等,则,
t=(5+3)÷1=8(秒),
而点Q的速度为:4÷8=0.5(cm/s),
∴所求时间为8秒,点Q的速度为0.5cm/s,
② 
由题意可知,RT△ABF≌RT△CDE,且AB=CD=4,BF=DE=3,AF=CE=5,
如图:当四边形APCQ是平行四边形时,有AP∥CQ,且AP=CQ,
而 AP=t,CQ=(3+4+5)﹣0.8t,则
t=12﹣0.8t,t=12,
即:当以点A、P、C、Q为顶点的四边形为平行四边形时,t的值为12
【解析】(1)由判定定理“对角线互相垂直的平行四边形是菱形”可证,(2)由(1)得,设AF=FC=CE=AE=x,BF=y,由图形中存在的等量关系及勾股定理求证,(3)①若以点A、C、P、Q四点为顶点四边形是矩形,则点P与点B重合,点Q与点D 重合,由运动过程中时间相等求解,②则利用平行四边形的性质可以求解.
【考点精析】掌握菱形的性质和矩形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).
(1)如图1,AB∥CD,∠B+∠D=180°,求证:CB∥DE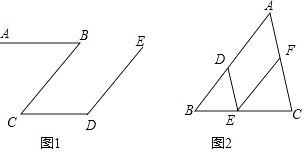
证明:∵AB∥CD(已知)
∴∠B=
∵∠B+∠D=180°(已知)
∴∠C+∠D=180°(等量代换)
∴∥
(2)如图2,已知DE∥AC,∠A=∠DEF,请证明∠B=∠FEC. 证明:∵DE∥AC(已知)
∴∠A=
∵∠A=∠DEF(已知)
∴∠DEF=∠(等量代换)
∴AB∥
∴∠=∠ . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算错误的是( )
A. (6a+1)(6a﹣1)=36a2﹣1 B. (a3﹣8)(﹣a3+8)=a9﹣64
C. (﹣m﹣n)(m﹣n)=n2﹣m2 D. (﹣a2+1)(﹣a2﹣1)=a4﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4).
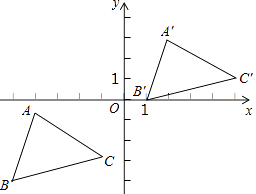
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知M=
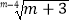 是m+3的算术平方根,N=
是m+3的算术平方根,N=  是n﹣2的立方根, 求:M﹣N的值的平方根.
是n﹣2的立方根, 求:M﹣N的值的平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知tanα=0.3249,则α约为( )
A.17°
B.18°
C.19°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC.
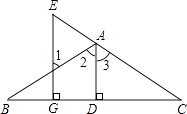
证明:∵AD⊥BC于D,EG⊥BC于G()
∴∠ADC=90°,∠EGC=90°()
∴∠ADC=∠EGC
∴AD∥EG()
∴∠1=∠2()
∠E=∠3()
又∵∠E=∠1()
∴∠2=∠3
∴AD平分∠BAC().
相关试题

