搜索
【题目】在△ABC中BC=2，AB=2 
，AC=b，且关于x的方程x2﹣4x+b=0有两个相等的实数根，则AC边上的中线长为 ．
参考答案：
【答案】2
【解析】解：∵关于x的方程x2﹣4x+b=0有两个相等的实数根， ∴△=16﹣4b=0，
∴AC=b=4，
∵BC=2，AB=2 
，
∴BC2+AB2=AC2 ，
∴△ABC是直角三角形，AC是斜边，
∴AC边上的中线长= 
AC=2；
所以答案是：2．
【考点精析】本题主要考查了求根公式和直角三角形斜边上的中线的相关知识点，需要掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根；直角三角形斜边上的中线等于斜边的一半才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查2000户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：
用户每月用水量（m3）
32及其以下
33
34
35
36
37
38
39
40
41
42
43及其以上
户数（户）
200
160
180
220
240
210
190
100
170
120
100
110
（1）为确保70%的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？
（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设x表示每户每月用水量（单位：m3），y表示每户每月应交水费（单位：元），求y与x的函数关系式；
（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？ -
科目： 来源： 题型：
查看答案和解析>>【题目】2017宁夏）在边长为2的等边三角形ABC中，P是BC边上任意一点，过点 P分别作 PM⊥A B，PN⊥AC，M、N分别为垂足．
（1）求证：不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；
（2）当BP的长为何值时，四边形AMPN的面积最大，并求出最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A在函数y1=﹣
（x＞0）的图象上，点B在直线y2=kx+1+k（k为常数，且k≥0）上．若A，B两点关于原点对称，则称点A，B为函数y1 ， y2图象上的一对“友好点”．请问这两个函数图象上的“友好点”对数的情况为（ ）
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目： 来源： 题型：
查看答案和解析>>【题目】我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率π的近似值，设半径为r的圆内接正n边形的周长为L，圆的直径为d，如图所示，当n=6时，π≈
= 
=3，那么当n=12时，π≈ = ． （结果精确到0.01，参考数据：sin15°=cos75°≈0.259） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O为等腰△ABC的外接圆，直径AB=12，P为弧
上任意一点（不与B，C重合），直线CP交AB延长线于点Q，⊙O在点P处切线PD交BQ于点D，下列结论正确的是 ． （写出所有正确结论的序号） ①若∠PAB=30°，则弧 
的长为π；②若PD∥BC，则AP平分∠CAB；
③若PB=BD，则PD=6
；④无论点P在弧 上的位置如何变化，CPCQ为定值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：2sin60°+|3﹣
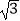|+（π﹣2）0﹣（ 
）﹣1 ．
相关试题
