【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”. 
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017
B.2016
C.191
D.190
参考答案:
【答案】D
【解析】解:找规律发现(a+b)3的第三项系数为3=1+2; (a+b)4的第三项系数为6=1+2+3;
(a+b)5的第三项系数为10=1+2+3+4;
不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),
∴(a+b)20第三项系数为1+2+3+…+20=190,
故选 D.
【考点精析】关于本题考查的完全平方公式,需要了解首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备为七年级同学庆祝最后一个“儿童节”,至少需要甲种鲜花266朵,乙种鲜花169朵,制成A、B两种造型共16束.要求A造型用甲种鲜花18朵,乙种鲜花10朵;B造型用甲种鲜花16朵,乙种鲜花11朵,送某花店制作.
(1)花店共有几种制作方案?分别有哪几种?
(2)若A种造型每束鲜花可获得利润12元,B种造型每束鲜花可获得利润10元.如果你是店主,你选择哪种制作方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,若点
,若点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿折线
个单位长度的速度沿折线 运动(回到点
运动(回到点 停止运动),设运动时间为
停止运动),设运动时间为 秒.
秒.(1)当点
 在
在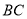 上时,且满足
上时,且满足 时,求出此时
时,求出此时 的值;
的值;(2)当点
 在
在 上时,求出
上时,求出 为何值时,
为何值时, 为以
为以 为腰的等腰三角形.
为腰的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+
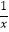 =3,则下列三个等式:①x2+
=3,则下列三个等式:①x2+ 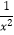 =7,②x﹣
=7,②x﹣ 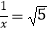 ,③2x2﹣6x=﹣2中,正确的个数有( )
,③2x2﹣6x=﹣2中,正确的个数有( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.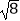 ﹣
﹣ 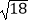 =﹣
=﹣ 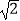
B.(﹣0.1)﹣2=0.01
C.(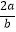 )2÷
)2÷ 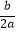 =
= 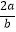
D.(﹣m)3?m2=﹣m6 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
问题发现:学完四边形的有关知识后,创新小组的同学进一步研究特殊的四边形,发现了一个结论.如图1,已知四边形
 是正方形,根据勾股定理和正方形的性质,很容易能够证明
是正方形,根据勾股定理和正方形的性质,很容易能够证明 .
.问题探究:
(1)如图2,已知四边形
 是矩形,若
是矩形,若 ,则
,则 的值是 ;
的值是 ; 的值是 ;
的值是 ;(2)如图3,已知四边形
 是菱形,证明:
是菱形,证明: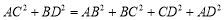 ;
;拓广探索:
(3)智慧小组看了创新小组交流后,提出了一个猜想,如图4,在
 中,
中,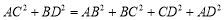 ,你认为这个猜想正确吗?请说明理由;
,你认为这个猜想正确吗?请说明理由;(4)请用文字语言叙述
 中得出的结论.
中得出的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )

A.55°
B.70°
C.125°
D.145°
相关试题

