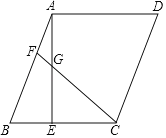
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
参考答案:
【答案】(1)![]() 1;(2)见解析.
1;(2)见解析.
【解析】
(1)在Rt△ABE中,由勾股定理求得BE,再由线段和差求得结果;
(2)延长GA到H,使得AH=BE,证明△ADH≌△EAB得DH=AB=CD,得∠DCH=∠DHC,再证明∠GHC=∠GCH得GC=GH便可得结果.
(1)∵CF=CB=AE,BC![]() ,
,
∴AE![]() ,
,
∵AE⊥BC于点E,AB![]() ,
,
∴BE![]() ,
,
∴CE=BC﹣BE![]() 1;
1;
(2)延长GA到H,使得AH=BE,连接DH,CH,
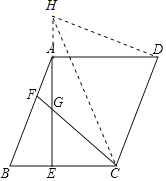
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE⊥BC,
∴∠AEB=∠DAE=90°,
∵BC=AE,
∴AE=DA,
在△ADH和△EAB中,
 ,
,
∴△ADH≌△EAB(SAS),
∴DH=DC,∠DHA=∠ABE,
∴∠DHC=∠DCH,
∵CB=CF,
∴∠CBF=∠CFB,
∵AB∥CD,
∴∠CFB=∠DCF,
∴∠CBF=∠DCF,
∵∠DHA=∠ABE,
∴∠DHA=∠DCF,
∵∠DHC=∠DCH,
∴∠CHG=∠HCG,
∴CG=HG,即CG=AG+AH,
∴AH=CG﹣AG,
∵AH=BE,
∴BE=CG﹣AG,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车去郊外春游,他离家的距离y(千米)与所用时间x(小时)之间的关系如图,根据图象回答:
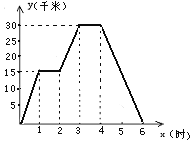
(1)小明到达离家最远的地方需几小时?此时离家多远?
(2)小明出发两个半小时时离家多远?
(3)小明出发多长时间离家12.5千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等边三角形,四边形ACFE是平行四边形,AE=BC.
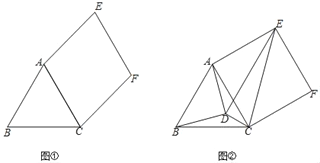
(1)如图①,求证:ACFE是菱形;
(2)如图②,点D是△ABC内一点,且∠ADB=90°,∠EDC=90°,∠ABD=∠ACE.求证:ACFE是正方形.
-
科目: 来源: 题型:
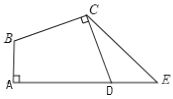
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列资料,解决问题:
定义:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:
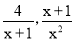 ,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如: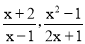 这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
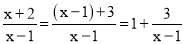 .
.(1)分式
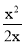 是 (填“真分式”或“假分式”);
是 (填“真分式”或“假分式”);(2)将假分式
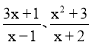 分别化为带分式;
分别化为带分式;(3)如果分式
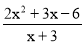 的值为整数,求所有符合条件的整数x的值.
的值为整数,求所有符合条件的整数x的值.
相关试题

