【题目】小明骑自行车去郊外春游,他离家的距离y(千米)与所用时间x(小时)之间的关系如图,根据图象回答:
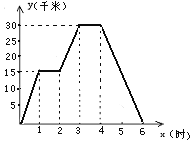
(1)小明到达离家最远的地方需几小时?此时离家多远?
(2)小明出发两个半小时时离家多远?
(3)小明出发多长时间离家12.5千米?
参考答案:
【答案】(1)小明到达离家最远的地方需3小时;此时他离家30千米;(2)出发两个半小时,小明离家22.5千米;(3)小明出发![]() 小时或
小时或![]() 小时距家12.5千米.
小时距家12.5千米.
【解析】
(1)根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需3小时;此时,他离家30千米;
(2)因为C(2,15)、D(3,30)在直线上,运用待定系数法求出解析式后,把x=2.5代入解析式即可;
(3)分别利用待定系数法求得过E、F两点的直线解析式,以及A、B两点的直线解析式.分别令y=12.5,求解x即可.
解:(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米;
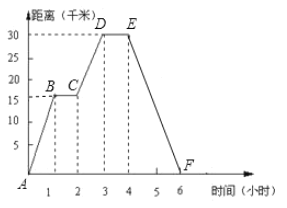
(2)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),
代入得:y=15x-15,(2≤x≤3),
当x=2.5时,y=22.5(千米);
答:出发两个半小时,小明离家22.5千米;
(3)设过E、F两点的直线解析式为y=k2x+b2,
由E(4,30)、F(6,0),代入得y=-15x+90,(4≤x≤6)
过A、B两点的直线解析式为y=k3x,
∵B(1,15),
∴y=15x(0≤x≤1);
当![]() 时,
时,
![]() ,解得:
,解得:![]() ;
;
![]() ,解得:
,解得:![]() ;
;
答:小明出发![]() 小时或
小时或![]() 小时距家12.5千米.
小时距家12.5千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)
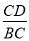 的值为 ________.
的值为 ________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是等边三角形,四边形ACFE是平行四边形,AE=BC.
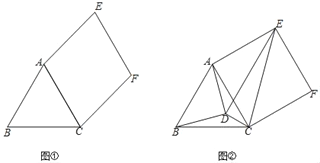
(1)如图①,求证:ACFE是菱形;
(2)如图②,点D是△ABC内一点,且∠ADB=90°,∠EDC=90°,∠ABD=∠ACE.求证:ACFE是正方形.
-
科目: 来源: 题型:
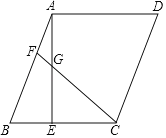
查看答案和解析>>【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB
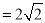 ,BC
,BC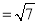 ,求CE的长;
,求CE的长;(2)求证:BE=CG﹣AG.
-
科目: 来源: 题型:
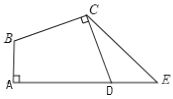
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.
相关试题

