【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
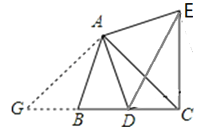
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

参考答案:
【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析
【解析】
试题(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;
(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.
试题解析:
解(1):(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为:垂直,相等;
②都成立,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
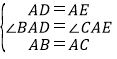
∴△DAB≌△EAC,
∴CE=BD,∠B=∠ACE,
∴∠ACB+∠ACE=90°,即CE⊥BD;
(2)当∠ACB=45°时,CE⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
在△GAD与△CAE中,

∴△GAD≌△CAE,
∴∠ACE=∠AGC=45°,
∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠DAE=∠BCF.

(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数. -
科目: 来源: 题型:
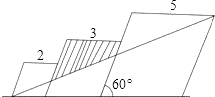
查看答案和解析>>【题目】已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
A.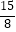
B.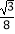
C.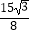
D.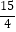
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
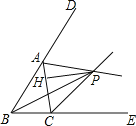
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的长方体.

(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A.1
B.2
C.3
D.4
相关试题

