【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于C、D两点,点P在直线CD上.
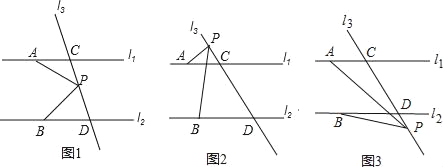
(1)试写出图1中∠APB、∠PAC、∠PBD之间的关系,并说明理由;
(2)如果P点在C、D之间运动时,∠APB、∠PAC、∠PBD之间的关系会发生变化吗?
答: (填发生或不发生)
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),如图2,图3,试分別写出∠PAC、∠APB、∠PBD之间的关系,并说明理由.
参考答案:
【答案】见试题解析
【解析】
试题(1)过点P作PE∥l1,∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,两个等式相加即可得出结论。(2)不发生(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:①如图1,有结论:∠APB=∠PBD-∠PAC. 理由如下:
过点P作PE∥l1,则∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以可得出结论∠APB=∠PBD-∠PAC.。
②如图2,有结论:∠APB=∠PAC-∠PBD. 理由如下:过点P作PE∥l2,则∠BPE=∠PBD,
又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,所以可得结论∠APB=∠PAC-∠PBD.
试题解析:解:(1)∠APB=∠PAC+∠PBD. 理由如下:
过点P作PE∥l1,
则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APE+∠BPE=∠PAC+∠PBD,
即∠APB=∠PAC+∠PBD.
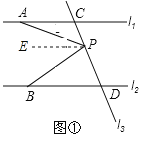
(2)若P点在C、D之间运动时∠APB=∠PAC+∠PBD这种关系不变.
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:
①如图1,有结论:∠APB=∠PBD-∠PAC. 理由如下:
过点P作PE∥l1,则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APB=∠BPE-∠APE,即∠APB=∠PBD-∠PAC.
②如图2,有结论:∠APB=∠PAC-∠PBD. 理由如下:
过点P作PE∥l2,则∠BPE=∠PBD,
又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,
所以∠APB=∠APE-∠BPE,即∠APB=∠PAC-∠PBD.
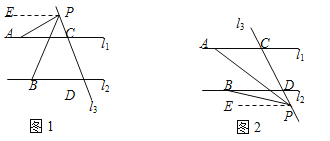
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班决定购买一些笔记本和文具盒做奖品.已知需要的笔记本数量是文具盒数量的3倍,购买的总费用不低于220元,但不高于250元.
(1)商店内笔记本的售价4元/本,文具盒的售价为10元/个,设购买笔记本的数量为x,按照班级所定的费用,有几种购买方案?每种方案中笔记本和文具盒数量各为多少?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)经过还价,老板同意4元/本的笔记本可打八折,10元/个的文具盒可打七折,用(2)中的最少费用最多还可以多买多少笔记本和文具盒?
-
科目: 来源: 题型:
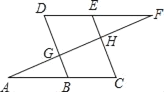
查看答案和解析>>【题目】如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
说明:
因为∠AGB=∠EHF(已知)
∠AGB= (依据: )
所以 ,(等量代换)
所以 (依据: )
所以∠C= ,(依据: )
又因为∠C=∠D,(已知)
所以 ,(等量代换)
所以DF∥AC(依据: )
所以∠A=∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“关联点”P’的坐标定义如下:当
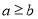 时,P’点坐标为(b,a);当
时,P’点坐标为(b,a);当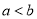 时,P’点坐标为(-a,-b).
时,P’点坐标为(-a,-b).(1)写出A(5,3)的变换点坐标_____,B(1,6)的变换点坐标______,C(-2,4)的变换点坐标_____;
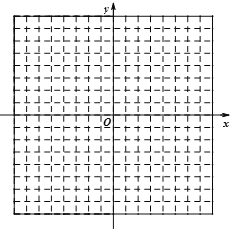
(2)如果直线l:
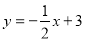 上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;
上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;(3)在(2)的条件下,若直线y=kx-1(k≠0)与图形W有两个交点,请直接写出k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程
例:若代数式
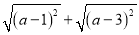 的值是
的值是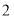 ,求
,求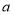 的取值范围.
的取值范围.解:原式=

当
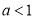 时,原式
时,原式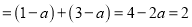 ,解得
,解得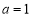 (舍去);
(舍去);当
 时,原式
时,原式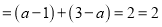 ,符合条件;
,符合条件;当
 时,原式
时,原式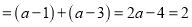 ,解得
,解得 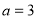 (舍去).
(舍去).所以,
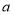 的取值范围是
的取值范围是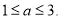
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
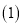 当
当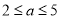 时,化简:
时,化简:
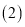 若等式
若等式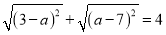 成立,则
成立,则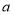 的取值范围是
的取值范围是  若
若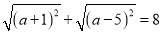 ,求
,求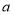 的取值.
的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
相关试题

