【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
参考答案:
【答案】(1)w=-x2+90x-1800;(2)当x=45时,w有最大值,最大值是225(3)该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元
【解析】试题分析:(1)销售利润=(销售单价-成本)×销售量,所以![]()
![]() ;(2)利用顶点式求二次函数极值,可求出每天最大利润;(3)把w=200带到解析式中,求出销售单价,把超过42元的舍掉.
;(2)利用顶点式求二次函数极值,可求出每天最大利润;(3)把w=200带到解析式中,求出销售单价,把超过42元的舍掉.
试题解析:(1)![]()
![]()
![]()
所以w与x的函数关系式为:![]() (30≤x≤60)
(30≤x≤60)
(2)![]() .
.
∵﹣1<0,
∴当x=45时,w有最大值.w最大值为225.
答:销售单价定为45元时,每天销售利润最大,最大销售利润225元.
(3)当w=200时,可得方程![]() .
.
解得x1=40,x2=50.
∵50>42,
∴x2=50不符合题意,应舍去.
答:该商店销售这种健身球每天想要获得200元的销售利润,销售单价应定为40元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合, 得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2. 折叠该纸片,探究MN与BM的数量关系.写出折叠方案, 并结合方案证明你的结论.

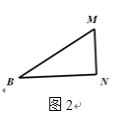
-
科目: 来源: 题型:
查看答案和解析>>【题目】n边形的每个外角都为24°,则边数n为________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=10,则S2的值是 .
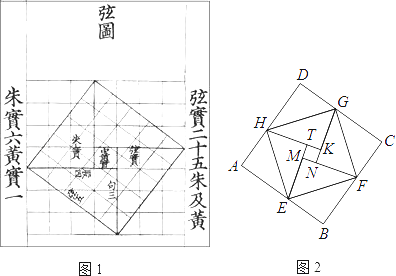
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们学习了四边形和一些特殊的四边形,如图表示了在某种条件下它们之间的关系.如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行.那么请你对标上的其他6个数字序号写出相对应的条件.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2﹣6x﹣5=0,此方程可化为( )
A. (x﹣3)2=4 B. (x﹣3)2=14 C. (x﹣9)2=4 D. (x﹣9)2=14
-
科目: 来源: 题型:
查看答案和解析>>【题目】在算式(﹣1)□(+2)的□中填上运算符号,使结果最小,这个运算符号是( )
A. 加号B. 减号C. 乘号D. 除号
相关试题

