【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
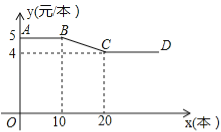
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
参考答案:
【答案】(1)购买不超过10本此种笔记本时售价为5元/本.(2)①当0<x≤10时,y=5;②当10<x≤20时,y=﹣0.1x+6;③当20<x时,y=4.(3)当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.
【解析】
试题(1)观察一次函数图象可知线段AB与x轴平行,即可得出线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本;(2)观察一次函数图象可知,图象分三段,因此y与x之间的函数关系式分三种情况,①当0<x≤10时,②当10<x≤20时,③当x>20时,根据这三种情况分别求出y与x之间的函数关系式即可;(3)根据题意求出W与x之间的关系式,再利用二次函数的性质即可求解.
试题解析: 解:(1)图中线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本.
(2)①当0<x≤10时,
y与x之间的函数关系式y=5,
②当10<x≤20时,
设=kx+b把B(10,5),C(20,4)代入得![]() ,
,
解得![]() .
.
所以y与x之间的函数关系式y=﹣0.1x+6.
③当x>20时,y与x之间的函数关系式为:y=4.
(3)W=(﹣0.1x+6﹣3)x=﹣0.1×(x﹣15)2+22.5.
答:当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2012年6月3号国际田联钻石联赛美国尤金站比赛中,百米跨栏飞人刘翔以12.87s的成绩打破世界记录并轻松夺冠.A、B两镜头同时拍下了刘翔冲刺时的画面(如图),从镜头B观测到刘翔的仰角为60°,从镜头A观测到刘翔的仰角为30°,若冲刺时的身高大约为1.88m,请计算A、B两镜头之间的距离为 . (结果保留两位小数,
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)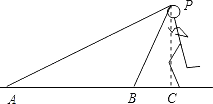
-
科目: 来源: 题型:
查看答案和解析>>【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣
 ,设点B所表示的数为m.
,设点B所表示的数为m. 
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=∠B=30°,CD平分∠ACB,M、N分别是BC、AC的中点.图中等于60°的角有( )个.
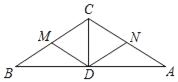
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.
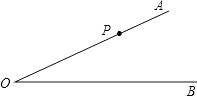
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部.
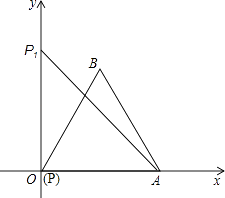
(1)当顶点P在射线OY上移动到点P1时,连接AP1 , 请用尺规作图;在∠XOY内部作出以AP1为边的等边△AP1B1(要求保留作图痕迹,不要求写作法和证明);
(2)设AP1交OB于点C,AB的延长线交B1P1于点D.求证:△ABC∽△AP1D;
(3)连接BB1 , 求证:∠ABB1=90°.
相关试题

