【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
参考答案:
【答案】(1)y=200﹣60x(0≤x≤![]() );(2)80.
);(2)80.
【解析】试题(1)因为剩余的路程=两地的距离﹣行驶的距离即可得到y与x的函数关系式,然后再求得汽车行驶200千米所需要的时间即可求得x的取值范围.
(2)将x=2代入函数关系式,求得y值即可.
试题解析:(1)y=200﹣60x(0≤x≤![]() );
);
(2)当x=2时,y=200﹣60×2=80千米.
答:汽车距离B地80千米.
-
科目: 来源: 题型:
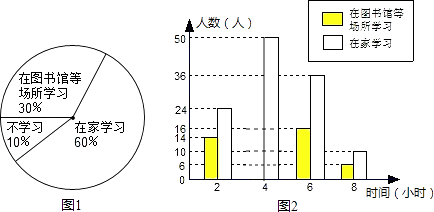
查看答案和解析>>【题目】崇左市江州区太平镇壶城社区调查居民双休日的学习状况,采取了下列调查方式;a:从崇左高中、太平镇中、太平小学三所学校中选取200名教师;b:从不同住宅楼(即江湾花园与万鹏住宅楼)中随机选取200名居民;c:选取所管辖区内学校的200名在校学生.并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图.以下结论:①上述调查方式最合理的是b;②在这次调查的200名教师中,在家学习的有60人;③估计该社区2000名居民中双休日学习时间不少于4小时的人数是1180人;④小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔不学习的概率是0.1.其中正确的结论是( )
A.①④
B.②④
C.①③④
D.①②③④ -
科目: 来源: 题型:
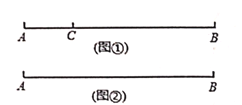
查看答案和解析>>【题目】如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是段AB的“2倍点”.
(1)线段的中点__________这条线段的“2倍点”;(填“是”或“不是”)
(2)若AB=15cm,点C是线段AB的“2倍点”.求AC的长;
(3)如图②,已知AB=20cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动.点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动.点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s),当t=_____________s时,点Q恰好是线段AP的“2倍点”.(请直接写出各案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2012年6月3号国际田联钻石联赛美国尤金站比赛中,百米跨栏飞人刘翔以12.87s的成绩打破世界记录并轻松夺冠.A、B两镜头同时拍下了刘翔冲刺时的画面(如图),从镜头B观测到刘翔的仰角为60°,从镜头A观测到刘翔的仰角为30°,若冲刺时的身高大约为1.88m,请计算A、B两镜头之间的距离为 . (结果保留两位小数,
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)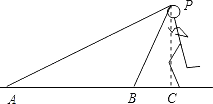
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣
 ,设点B所表示的数为m.
,设点B所表示的数为m. 
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
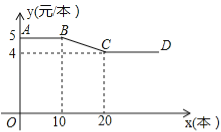
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=∠B=30°,CD平分∠ACB,M、N分别是BC、AC的中点.图中等于60°的角有( )个.
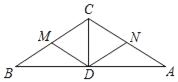
A. 3 B. 4 C. 5 D. 6
相关试题

