【题目】如图所示,在△ABC中,∠A=∠B=30°,CD平分∠ACB,M、N分别是BC、AC的中点.图中等于60°的角有( )个.
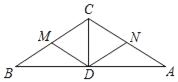
A. 3 B. 4 C. 5 D. 6
参考答案:
【答案】D
【解析】
由题意可得△ABC是等腰三角形,且M、N分别是BC、AC的中点,根据直角三角形斜边上的中线等于斜边的一半可求BM=MD=MC,CN=AN=DN,可证△CMD,△CND是等边三角形,即可求等于60°的角的个数.
∵∠B=∠A=30°,∴BC=AC.
又∵CD平分∠BCA,∴CD⊥AB.
∵CD⊥AB,M、N分别是BC、AC的中点,∴BM=MC=MD,DN=CN=NA,∴∠B=∠MDB=30°,∴∠CMD=∠B+∠MDB=60°.
∵MC=MD,∠CMD=60°,∴△MCD是等边三角形,∴∠MCD=∠MDC=∠DMC=60°.
同理可证:△MCD是等边三角形,∴∠CND=∠NCD=∠CDN=60°,∴等于60°的角有6个.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣
 ,设点B所表示的数为m.
,设点B所表示的数为m. 
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
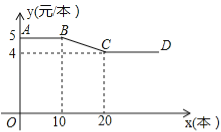
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.
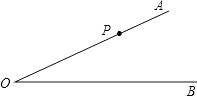
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部.
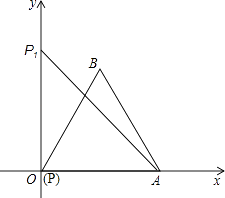
(1)当顶点P在射线OY上移动到点P1时,连接AP1 , 请用尺规作图;在∠XOY内部作出以AP1为边的等边△AP1B1(要求保留作图痕迹,不要求写作法和证明);
(2)设AP1交OB于点C,AB的延长线交B1P1于点D.求证:△ABC∽△AP1D;
(3)连接BB1 , 求证:∠ABB1=90°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
相关试题

