【题目】两个一次函数y1=ax+b与y2=bx+a,它们在同一直角坐标系中的图象可能是( )
A.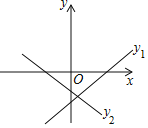 B.
B.
C. D.
D.
参考答案:
【答案】C
【解析】
A、∵一次函数y1=ax+b的图象经过第一、三、四象限,∴a>0,b<0;
由一次函数y2=bx+a图象可知,b<0,a<0,两结论矛盾,故错误;
B、∵一次函数y1=ax+b的图象经过第一、二、三象限,∴a>0,b>0;
由y2的图象可知,a>0,b<0,两结论相矛盾,故错误;
C、∵一次函数y1=ax+b的图象经过第一、三、四象限,∴a>0,b<0;
由y2的图象可知,a>0,b<0,两结论不矛盾,故正确;
D、∵一次函数y1=ax+b的图象经过第一、二、三象限,∴a<0,b>0;
由y2的图象可知,a<0,b<0,两结论相矛盾,故错误.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
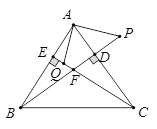
求证:(1)AP=AQ ;
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为 2000 元,1700 元的A,B两种型号的净水器,下表是近两周的销售情况:
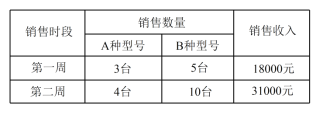
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台,求 A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.
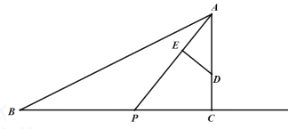
(1)当t=3秒时,求AP的长度(结果保留根号);
(2)当△ABP为等腰三角形时,求t的值;
(3)过点D做DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
-
科目: 来源: 题型:
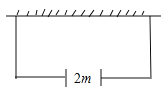
查看答案和解析>>【题目】如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米?
(2)围成鸡场的面积可能达到200平方米吗?
相关试题

