【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

参考答案:
【答案】(1)经过2秒或4秒,△PBQ的面积等于8cm2;(2)线段PQ不能否将△ABC分成面积相等的两部分;(3)经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.
【解析】【试题分析】(1)设经过x秒,使△PBQ的面积等于8cm2,则PB=6-x,BQ=2x,列方程为: ![]() ,解得x1=2,x2=4,;(2)先计算△ABC的面积=
,解得x1=2,x2=4,;(2)先计算△ABC的面积=![]() ×6×8=24,
×6×8=24,
设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
![]() ,变形得,y2﹣6y+12=0,则△=b2﹣4ac=36﹣4×12=﹣12<0,即此方程无实数根,即线段PQ不能否将△ABC分成面积相等的两部分;
,变形得,y2﹣6y+12=0,则△=b2﹣4ac=36﹣4×12=﹣12<0,即此方程无实数根,即线段PQ不能否将△ABC分成面积相等的两部分;
(3)分类讨论,三种情况:
①点P在线段AB上,点Q在线段CB上(0<m<4),
设经过m秒,依题意列方程得: ![]()
m2﹣10m+23=0,
解得m1=5+![]() ,m2=5﹣
,m2=5﹣![]() ,
,
经检验,m1=5+![]() 不符合题意,舍去,
不符合题意,舍去,
∴m=5﹣![]() ;
;
②点P在线段AB上,点Q在射线CB上(4<n<6),
设经过n秒,依题意有
![]() ,
, ![]()
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(k>6),设经过k秒,依题意有
![]() (k﹣6)(2k﹣8)=1,k2﹣10k+23=0,
(k﹣6)(2k﹣8)=1,k2﹣10k+23=0,
解得k1=5+![]() ,k2=5﹣
,k2=5﹣![]() ,经检验,k1=5﹣
,经检验,k1=5﹣![]() 不符合题意,舍去,
不符合题意,舍去,
∴k=5+![]() ;综上所述,经过(5﹣
;综上所述,经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.
【试题解析】
(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
![]() (6﹣x)2x=8,
(6﹣x)2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=![]() ×6×8=24,
×6×8=24,
![]() (6﹣y)2y=12,
(6﹣y)2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=364×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<x<4),
设经过m秒,依题意有
![]() (6﹣m)(8﹣2m)=1,
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+![]() ,m2=5﹣
,m2=5﹣![]() ,
,
经检验,m1=5+![]() 不符合题意,舍去,
不符合题意,舍去,
∴m=5﹣![]() ;
;
②点P在线段AB上,点Q在射线CB上(4<x<6),
设经过n秒,依题意有
![]() (6﹣n)(2n﹣8)=1,
(6﹣n)(2n﹣8)=1,
m2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(x>6),
设经过k秒,依题意有
![]() (k﹣6)(2k﹣8)=1,
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+![]() ,k2=5﹣
,k2=5﹣![]() ,
,
经检验,k1=5﹣![]() 不符合题意,舍去,
不符合题意,舍去,
∴k=5+![]() ;
;
综上所述,经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:
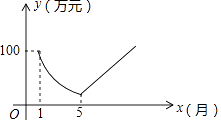
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月? -
科目: 来源: 题型:
查看答案和解析>>【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足|x1|+|x2|=|x1x2|-1,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.
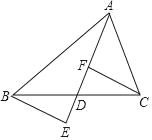
(1)求证:DE=DF;
(2)若在原有条件基础上再添加AB=AC,你还能得出什么结论.(不用证明)(写2个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y=
 x与y=
x与y= 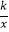 (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= x与y=
x与y= 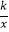 ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程: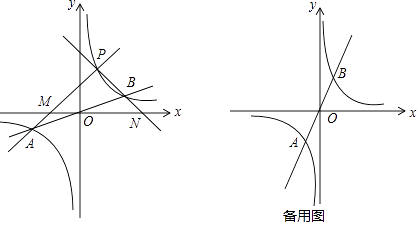
(1)如图所示,设函数y= x与y=
x与y= 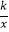 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则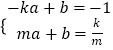 ,
,
解得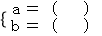
∴直线PA的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:
①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )个.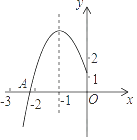
A.1
B.2
C.3
D.4
相关试题

