搜索
【题目】等边三角形ABC 中，BD是角平分线，点E在BC边的延长线上，且CD=CE，则∠BDE的度数是（ ）
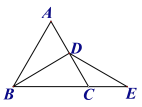
A.90°B.100°C.120°D.无法确定
参考答案：
【答案】C
【解析】
根据等边三角形的性质可得∠ACB=60°，∠DBC=30°，根据CD=CE可得∠CDE=∠CED，根据∠CDE+∠CED=∠ACB即可求得∠CED=30°．进而可得到∠BDE的度数.
解：∵三角形ABC是等边三角形，BD是角平分线，
∴∠ACB=60°，∠DBC=
∠ABC= 30°，
∵CD=CE，
∴∠CDE=∠CED，
∵∠CDE+∠CED=∠ACB
∴∠CED=30°，
∴∠BDE=180°-∠DBC-∠CED
=180°-30°-30°
=120°
故选：C
-
科目： 来源： 题型：
查看答案和解析>>【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：
星期
一
二
三
四
五
六
日
增减
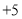
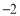
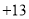
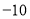
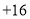
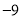
（1）根据记录可知前三天共生产______辆．
（2）产量最多的一天比产量最少的一天多生产_______辆．
（3）该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于整式
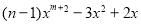（其中m是大于
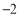的整数）.（1）若
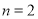，且该整式是关于x的三次三项式，求m的值；（2）若该整式是关于x的二次单项式，求m，n的值；
（3）若该整式是关于x的二次二项式，则m，n要满足什么条件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=3ax2+2bx+c，
（1）若a=3k，b=5k，c=k+1，试说明此类函数图象都具有的性质；
（2）若a=
， c=2+b且抛物线在﹣2≤x≤2区间上的最小值是﹣3，求b的值；（3）若a+b+c=1，是否存在实数x，使得相应的y的值为1，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2-2ax+b经过点C（0，-
），且与x轴交于点A、点B，若tan
ACO=
．
（1）求此抛物线的解析式；
（2）若抛物线的顶点为M，点P是线段OB上一动点（不与点B重合），
MPQ=45
，射线PQ与线段BM交于点Q，当△MPQ为等腰三角形时，求点P的坐标． -
科目： 来源： 题型：
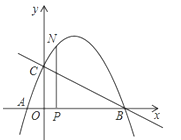
查看答案和解析>>【题目】如图，抛物线与x轴交于点A（﹣
， 0），点B（2，0），与y轴交于点C（0，1），连接BC．（1）求抛物线的解析式；
（2）N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t（﹣
＜t＜2），求△ABN的面积s与t的函数解析式；（3）若0＜t＜2且t≠0时，△OPN∽△COB，求点N的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用
，
表示直角三角形的两直角边
，下列四个说法：①
；②
；③
；④
；其中说法正确的是
A. ①②B. ①②③C. ①②④D. ①②③④
相关试题
