【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
参考答案:
【答案】D
【解析】
大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49;小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x-y=2;其中④由2xy+4=49可得2xy=45①,又由x2+y2=49②,可得![]() ;还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即
;还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即![]() ,化简得④2xy+4=49;从而求解.
,化简得④2xy+4=49;从而求解.
解:如图
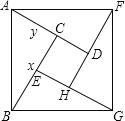
①![]() 为直角三角形,
为直角三角形,
![]() 根据勾股定理:
根据勾股定理:![]() ,
,
故本选项正确;
②由图可知,![]() ,
,
故本选项正确;
③由![]() 可得
可得![]() ①,
①,
又![]() ②,
②,
![]() ①
①![]() ②得,
②得,![]() ,
,
整理得,![]() ,
,
![]() ,
,
故本选项正确.
④由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,列出等式为![]() ,
,
即![]() ;
;
故本选项正确;
![]() 正确结论有①②③④.
正确结论有①②③④.
故选:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
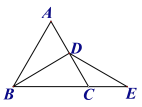
A.90°B.100°C.120°D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2-2ax+b经过点C(0,-
 ),且与x轴交于点A、点B,若tan
),且与x轴交于点A、点B,若tan ACO=
ACO= .
.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为M,点P是线段OB上一动点(不与点B重合),
 MPQ=45
MPQ=45 ,射线PQ与线段BM交于点Q,当△MPQ为等腰三角形时,求点P的坐标.
,射线PQ与线段BM交于点Q,当△MPQ为等腰三角形时,求点P的坐标. -
科目: 来源: 题型:
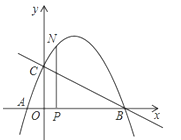
查看答案和解析>>【题目】如图,抛物线与x轴交于点A(﹣
 , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣
 <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
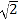 ≈1.4,
≈1.4, 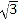 ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上点F处,折痕为BE,再沿过点E的直线折叠,使点D落在BE边上点D’处,折痕为EG,展平纸片,则图中∠FEG= ______ °
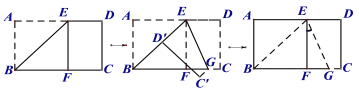
-
科目: 来源: 题型:
查看答案和解析>>【题目】为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).

(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);
(2)山高DC是多少(结果保留根号形式)?
相关试题

