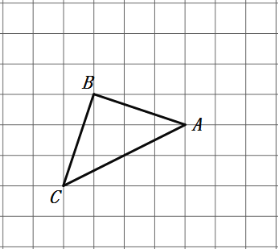
【题目】 如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线CD;
(2)过点B画直线AC的垂线,并注明垂足为G;
(3)线段 的长度是点B到直线AC的距离;线段BC的长度是 的距离;
(4)因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以线段BC、BG的大小关系为:BC BG.
(5)计算格点△ABC的面积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)BG,点C到直线AB;(4)![]() ;(5)
;(5)![]()
【解析】
(1)利用网格特点画CD![]() AB;
AB;
(2)易得![]() 为等腰直角三角形,则取
为等腰直角三角形,则取![]() 中点
中点![]() ,可得到
,可得到![]() ;
;
(3)直线外一点到直线的垂线段的长度,叫做点到直线的距离,据此可得答案;
(4)根据“垂线段最短”可得答案;
(5)根据:矩形面积减去三个三角形的面积即可.
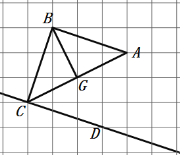
(1)如图所示:![]() 即为所求;
即为所求;
(2)如图所示:![]() 即为所求;
即为所求;
(3) 线段![]() 的长度是点B到直线AC的距离;线段BC的长度是点C到直线AB的距离;
的长度是点B到直线AC的距离;线段BC的长度是点C到直线AB的距离;
故答案为:BG,点C到直线AB;
(4) 因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以线段BC、BG的大小关系为:![]() .
.
故答案为:![]()
(5)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,
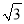 ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于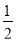 AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )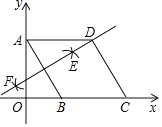
A. (2,2)B. (2,
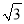 )C. (
)C. (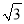 ,2)D. (
,2)D. (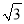 +1,
+1,
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点M、N表示的数分别为a、b,我们把a、b之差的绝对值叫做点M、N之间的距离,即MN=│a-b│.已知数轴上三点A、O、B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
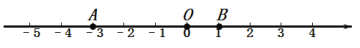
(1)如果点P到点A、点B的距离相等,那么x=_______;
(2)当x是多少时,点P到点A、点B的距离之和是6;
(3)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动,点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动几秒时,点P到点E、点F的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,过点B作直线l,点E在直线l上,连接CE,DE,CE=BC,过点C作CF⊥DE于点F,交直线l于点H,当l在如图①的位置时,易证:BH+EH=
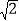 CH(不需证明).
CH(不需证明).(1)当l在如图②的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,并给予证明;
(2)当l在如图③的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,不必证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
10
2 000
10
5
2 500
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
-
科目: 来源: 题型:
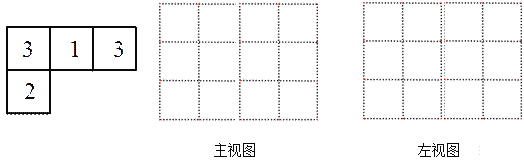
查看答案和解析>>【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
-
科目: 来源: 题型:
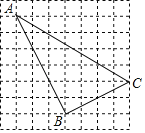
查看答案和解析>>【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
相关试题

