Question

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：
①abc＞0；②b＜a+c；③4a﹣2b+c＞0；④2c＜3b；⑤当m≤x≤m+1时，函数的最大值为a+b+c，则0≤m≤1；
其中正确的结论有（ ）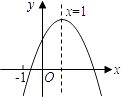

A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】B
【解析】解：①∵抛物线的对称轴为x=﹣ =1，

∴b=﹣2a．

∵抛物线开口向下，

∴a＜0，b＞0．

∵抛物线与y轴的交点在y轴正半轴，

∴c＞0，

∴abc＜0，结论①错误；

②当x=﹣1时，y=a﹣b+c＜0，

∴a+c＜b，结论②错误；

③当x=﹣2时，y=4a﹣2b+c＜0，

∴结论③错误；

④∵a+c＜b，b=﹣2a，

∴c＜b﹣a= b，

∴2c＜3b，结论④正确；

⑤∵抛物线的顶点坐标为（1，a+b+c），且a＜0，

∴当m≤x≤m+1时，函数的最大值为a+b+c，则0≤m≤1，

∴结论⑤正确．

综上所述：正确的结论有④⑤．

所以答案是：B．

【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系和二次函数的最值的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．