【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分别是AC,AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF , 则AE=;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
参考答案:
【答案】
(1)![]()
(2)解:设AE=x,则CE=4﹣x.
由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE.
∴∠AEF=∠AFE.
∴AE=AF.
∴AE=EM=MF=AF,
∴四边形AEMF为菱形.
∴EM∥AB.∴△CME∽△CBA.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,即AE=
,即AE= ![]()
(3)解:设AE=y,则CE=4﹣y.
由折叠可知:AE=EN=y,AF=NF,
∵NF⊥AB,
∴∠NFB=90°.
∵∠ACB=90°,
∴∠NFB=∠ACB.
且∠NBF=∠ABC,
∴△NBF∽ABC.
∴ ![]() =
= ![]() =
= ![]() .即BF=
.即BF= ![]() NF=
NF= ![]() AF.由BF+AF=AB=5,
AF.由BF+AF=AB=5,
解得:BF= ![]() ,NF=
,NF= ![]() ,
,
∴BN= ![]() =
= ![]() ,
,
∴CN=BN﹣BC= ![]() ﹣3=
﹣3= ![]() .
.
在Rt△CEN中,由勾股定理得:CN2+CE2=EN2,
∴( ![]() )2+(4﹣y)2=y2,
)2+(4﹣y)2=y2,
解得:y= ![]() ,
,
即AE= ![]()
【解析】解:(1)∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF≌S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴ ![]() =(
=( ![]() )2,即(
)2,即( ![]() )2=
)2= ![]() ,
,
∴AE= ![]() ;
;
所以答案是: ![]() ;
;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
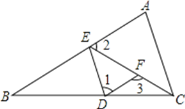
查看答案和解析>>【题目】如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=65°,
(1)AB与DF平行吗?说明理由;
(2)求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB,BC分别交于点D,E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.
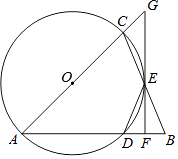
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
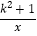 的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )A. y1>y2>y3B. y2>y1>y3C. y3>y1>y2D. y3>y2>y1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴、y轴分别交于点A,B,另一直线
与x轴、y轴分别交于点A,B,另一直线 与x轴、y轴分别交于点C,D,两直线相交于点M.
与x轴、y轴分别交于点C,D,两直线相交于点M. 求点M的坐标;
求点M的坐标; 连接AD,求△AMD的面积.
连接AD,求△AMD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题
5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a﹣2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )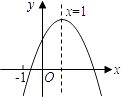
A.1个
B.2个
C.3个
D.4个
相关试题

