【题目】在△ABC中,BC=3 ![]() ,AC=5,∠B=45°,对于下面四个结论:
,AC=5,∠B=45°,对于下面四个结论:
①∠C一定是钝角; ②△ABC的外接圆半径为3;③sinA= ![]() ;④△ABC外接圆的外切正六边形的边长是
;④△ABC外接圆的外切正六边形的边长是 ![]() .其中正确的个数是( )
.其中正确的个数是( )
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:如图1,过C作CD⊥AB于D,过A作AE⊥BC于E,

∵∠B=45°,
∴△BDC是等腰直角三角形,
∵BC=3 ![]() ,
,
∴BD=CD=3,
由勾股定理得:AD= ![]() =
= ![]() =4,
=4,
∴sin∠BAC= ![]() =
= ![]() ,
,
所以③正确;
由S△ABC= ![]() ABCD=
ABCD= ![]() CBAE,
CBAE,
∴7×3=3 ![]() AE,
AE,
AE= ![]() =
= ![]() ,
,
在Rt△ABE中,
BE= ![]() =
= ![]() =
= ![]() >BC=3
>BC=3 ![]() =
= ![]() ,
,
∴∠ACB>90°,
即∠C一定是钝角;
所以①正确;
如图2,设△ABC的外接圆的圆心为O,连接OA、OC,
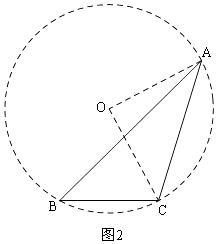
∵∠B=45°,
∴∠AOC=2∠B=90°,
∵OA=OC,
∴△AOC是等腰直角三角形,
∵AC=5,
∴OA= ![]() =
= ![]() ,
,
则△ABC的外接圆半径为 ![]() ;
;
所以②不正确;
如图3,此正六边形是△ABC的外接圆的外切正六边形,
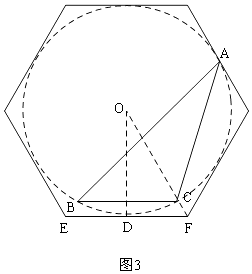
Rt△ODF中,由②得:OD= ![]() ,
,
由题意得:△OEF是等边三角形,
∴∠OFE=60°,
tan60°= ![]() =
= ![]() ,
,
∴EF=2DF= ![]() ,
,
则△ABC外接圆的外切正六边形的边长是 ![]() ,
,
所以④正确,
故本题正确的结论有:①③④;3个;
所以答案是:C.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握正多边形和圆(圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题
5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a﹣2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )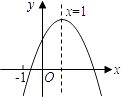
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=﹣5
D.x1=﹣1,x2=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足
 +|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.
+|b-2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.(1)则a=____,b=____;点C坐标为________;
(2)如下图所示:点D(m, n)在线段BC上,求m、n满足的关系式;

(3)如下图所示:E是线段OB上一动点,以OB为边作∠G=∠AOB,,交BC于点G,连CE交OG于点F,的当点E在线段OB上运动过程中,
 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.
的值是否会发生变化?若变化请说明理由,若不变,请求出其值.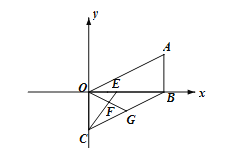
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
相关试题

