【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() 分别于
分别于![]() 、
、![]() 相切,则
相切,则![]() 的半径为( )
的半径为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
由勾股定理求出AB=10,连接FP、PE,过P作PM⊥AC于M,根据切线的性质得出矩形CMPF,推出PM=CF,PF=CM,设圆P的半径是r,根据切线的性质和切线长定理、等腰三角形的性质得到DF=FP,AM=PM,BE=BF,根据勾股定理得出AP2=AE2+PE2=AM2+PM2,代入即可得到方程,求出方程的解即可.
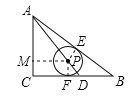
由勾股定理得:AB=![]() =10,
=10,
连接FP、PE,过P作PM⊥AC于M,
∵∠C=90°,PF⊥BC,
∴四边形CMPF是矩形,
∴PM=CF,PF=CM,
设圆P的半径是r,
∵AC=CD,∠C=90°,
∴∠ADC=45°,
∵PF⊥BC,
∴∠FPD=45°=∠ADC,
∴DF=FP=r,
同理:AM=PM,
∵圆P切AB于E,切BC于F,
∴BF=BE=BD+DF=8-6+r,
∴AE=10-(8-6+r)=8-r,
由勾股定理得:AP2=AE2+PE2=AM2+PM2,
∴(6-r)2+(6-r)2=r2+(8-r)2,
解得:r=1,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 中,点
中,点 在
在 边上,
边上, 交边
交边 于点
于点 ,且
,且 平分
平分 .
.(1)求证:
 ;
;(2)如图2,在
 边上取点
边上取点 ,使
,使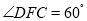 ,若
,若 ,
, ,求
,求 的长。
的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).

(1)当t为何值时,△PBQ是直角三角形?
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,点
,点 在第一象限,
在第一象限, 为等边三角形,
为等边三角形,
 ,垂足为点
,垂足为点 .
.
 ,垂足为
,垂足为 .
.
(1)求OF的长;
(2)作点
 关于
关于 轴的对称点
轴的对称点 ,连
,连 交
交 于E,求OE的长.
于E,求OE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为________;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为________个单位长度.(在图形中标出点P)

-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形
 的两条直角边
的两条直角边 、
、 的长分别是
的长分别是 和
和 ,则此直角三角形外接圆半径为________
,则此直角三角形外接圆半径为________ ,内切圆半径为________
,内切圆半径为________ .
.
相关试题

