【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 为等边三角形,
为等边三角形,![]()
![]() ,垂足为点
,垂足为点![]() .
.![]()
![]() ,垂足为
,垂足为![]() .
.

(1)求OF的长;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() 交
交![]() 于E,求OE的长.
于E,求OE的长.
参考答案:
【答案】(1)6;(2)2.
【解析】
(1)先过点B作BH⊥OA,垂足为F.由等腰三角形三线合一的性质可知OF=AF=4、BC=AC,根据等边三角形的性质可得:∠BOF=60°,根据特殊锐角三角函数值可得FB=![]() ,从而得到点B的坐标为(4,
,从而得到点B的坐标为(4,![]() ),再根据中点坐标公式可得点C的坐标为(6,
),再根据中点坐标公式可得点C的坐标为(6,![]() ),从而得到OF的长度;
),从而得到OF的长度;
(2)连接CD,交OB于G.由关于y轴对称的点的坐标特点可知:CD∥OA,D(6,![]() ),从而得到DC=12,由题意可知△BCG为等边三角形,从而得到CG=4,然后可求得DG=124=8=OA,依据AAS可证明△DEG≌△AEO,由全等三角形的性质可知OE=EG,从而求得OE的长度.
),从而得到DC=12,由题意可知△BCG为等边三角形,从而得到CG=4,然后可求得DG=124=8=OA,依据AAS可证明△DEG≌△AEO,由全等三角形的性质可知OE=EG,从而求得OE的长度.
解:(1)如图所示:过点B作BH⊥OA,垂足为H.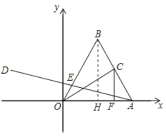
∵OB=AB,BH⊥OA,
∴OH=AH=4.
∵△OAB为等边三角形,
∴∠BOH=60°.
∴HB=OBsin60°=8×![]() =
=![]() .
.
∴点B的坐标为(4,![]() ).
).
∵AO=OB,OC⊥AB,
∴BC=AC.
由中点坐标公式可知点C的坐标为(6,![]() ).
).
∴OF=6;
(2)如图所示:连接CD,交OB于G.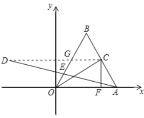
∵点C与点D关于y轴对称,
∴CD∥OA,点D(6,![]() ).
).
∴△BCG为等边三角形,
∴CG=![]() 4,CD=12.
4,CD=12.
∴DG=124=8=OA.
在△DEG和△AEO中,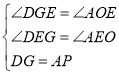
∴△DEG≌△AEO(AAS),
∴OE=EG=![]() OG,
OG,
∵BG=BC=![]() 4,
4,
∴OG=4,
∴OE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中,装有红球、白球、黄球共12个,这些球除颜色外完全相同,
从中随机摸出一个球,则:
(1)若盒子中有红球3个,则摸到红球的概率为_________;
(2)若摸到黄球的概率为
 ,则该盒子中装有黄球的个数是__________个;
,则该盒子中装有黄球的个数是__________个;(3)若将这12个球分别标上1至12这十二个数字,则摸到的数字是0的概率为________;摸到的数字是偶数的概率为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 是
是 边上的一个动点(点
边上的一个动点(点 不与点
不与点 ,点
,点 重合),在
重合),在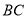 上取一点
上取一点 ,且∠CDE=50°.
,且∠CDE=50°.
(1)当
 时,求证:
时,求证: ;
;(2)当
 是等腰三角形时,
是等腰三角形时, 的度数为
的度数为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠C = 90°,
 .D为BC上一点,且到A,B两点的距离相等.
.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B = 35°,求∠CAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市甲、乙两支龙舟队在端午节期间进行划龙舟比赛,从起点
 驶向终点
驶向终点 ,在整个行程中,龙舟离开起点的距离
,在整个行程中,龙舟离开起点的距离 (米)与时间
(米)与时间 (分钟)的对应关系如图所示,根据图象所提供的信息解答下列问题:
(分钟)的对应关系如图所示,根据图象所提供的信息解答下列问题:(1)起点
 与终点
与终点 之间相距________米;
之间相距________米;(2)甲龙舟的速度是每分钟________米,乙龙舟的速度是每分钟___________米;
(3)图中
 ____________;
____________; _______________;
_______________;(4)乙龙舟在距终点1000米时,甲龙舟距终点的距离是______________米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广,为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写大赛”
 为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:成绩
 分
分
频数
 人
人
频率

10

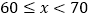
30


40
n
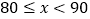
m


50

a
1
请根据所给信息,解答下列问题:
 ______,
______, ______,
______, ______;
______; 补全频数直方图;
补全频数直方图; 这若干名学生成绩的中位数会落在______分数段;
这若干名学生成绩的中位数会落在______分数段; 若成绩在90分以上
若成绩在90分以上 包括90分
包括90分 的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
相关试题

