【题目】若直角三角形![]() 的两条直角边
的两条直角边![]() 、
、![]() 的长分别是
的长分别是![]() 和
和![]() ,则此直角三角形外接圆半径为________
,则此直角三角形外接圆半径为________![]() ,内切圆半径为________
,内切圆半径为________![]() .
.

参考答案:
【答案】6.52
【解析】
(1)首先根据90°所对的弦是直径,因而利用勾股定理求出Rt△ABC斜边AB的长,即为直径,那么半径也即可得知.
(2)假设Rt△ABC内切圆P的半径为r,通过图可观察得到内切圆半径与Rt△ABC各边间的关系,列出关系式13=17-2r.从而解得r即为所求.
(1)在Rt△ABC内,AB=![]() (cm),
(cm),
∵AB是Rt△ABC外接圆的直径,
∴Rt△ABC外接圆的半径为6.5(cm),
(2)设Rt△ABC内切圆P的半径为r.
AE=AM=AC-r=5-r,BE=BN=BC-r=12-r,
AB=AE+BE=(5-r)+(12-r)=17-2r,
∴13=17-2r,
即r=2,
故答案为6.5,2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点, 为
为 上一点,且
上一点,且 ,
, 分别于
分别于 、
、 相切,则
相切,则 的半径为( )
的半径为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为________;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为________个单位长度.(在图形中标出点P)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是等边三角形ABC的角平分线,E是BC延长线上的一点,且CE=CD,DF=BC,垂足为F.BF与EF相等吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
 和
和 中,
中, 为
为 边
边 上一点,
上一点, 平分
平分 ,
,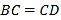 ,
, .
. 
(1)求证:

(2)如图(2),若
 ,连接
,连接 交
交 于
于 ,
, 为边
为边 上一点,满足
上一点,满足 ,连接
,连接 交
交 于
于 . ①求
. ①求 的度数;
的度数; ②若
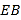 平分
平分 ,试说明:
,试说明: 平分
平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
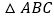 的边
的边 为直径画圆,与边
为直径画圆,与边 交于
交于 ,与边
,与边 交于
交于 ,已知
,已知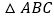 的面积是
的面积是 面积的
面积的 倍,
倍, 中有一个内角度数是另一内角度数的
中有一个内角度数是另一内角度数的 倍,试计算
倍,试计算 三个内角的度数:________.
三个内角的度数:________.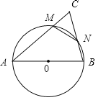
相关试题

