Question

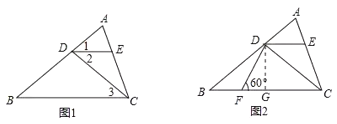
【题目】如图1，已知中，点在边上，交边于点，且平分．

(1)求证：；

(2)如图2，在边上取点，使，若，，求的长。

Answer 1

【答案】（1）见解析；（2）DF＝3．

【解析】

（1）如图，根据平行线的性质可得∠1＝∠B，∠2＝∠3，根据角平分线的定义可得∠1＝∠2，等量代换得到∠B＝∠3，即可证明DB＝DC；

（2）作DG⊥BC于点G，易求GB、GF的长，再根据在直角三角形中30°的锐角所对的直角边是斜边的一半即可求出DF的长．

解：（1）如图，∵DE∥BC，

∴∠1＝∠B，∠2＝∠3，

∵DE平分∠ADC，

∴∠1＝∠2，

∴∠B＝∠3，

∴DB＝DC；

（2）作DG⊥BC于点G，

∵DB＝DC，DG⊥BC，

∴GB＝BC＝×7＝3.5，

∴GF＝GBBF＝3.52＝1.5，

∵Rt△DGF中，∠DFG＝60°，

∴∠FDG＝30°，

∴DF＝2GF＝2×1.5＝3．